Search any question & find its solution
Question:
Answered & Verified by Expert
In the figure, a ray of light is perpendicular to the face $A B$ of a glass prism $(\mu=1.52)$.
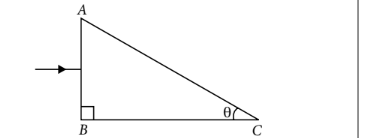
Find the value of $\theta$ so that the ray is totally reflected at face $A C$, if the prism is immersed in water $(\mu=1.33)$. Given $\sin 61^{\circ}=0.875$
Options:

Find the value of $\theta$ so that the ray is totally reflected at face $A C$, if the prism is immersed in water $(\mu=1.33)$. Given $\sin 61^{\circ}=0.875$
Solution:
1133 Upvotes
Verified Answer
The correct answer is:
$30^{\circ}$
Given, $\mu_g=1.52, \mu_w=1.33, \theta=$ ?
Apply Snell's law at point $D$,
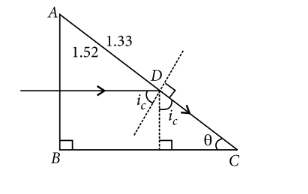
$\begin{aligned} & \mu_g \sin i_c=\mu_w \sin 90^{\circ} \\ & \Rightarrow \sin i_c=\frac{\mu_w}{\mu_g}=\frac{1.33}{1.52}\end{aligned}$
$\Rightarrow \quad i_c=\sin ^{-1}\left(\frac{1.33}{1.52}\right)=61^{\circ}$
From figure, $\theta+i_c=90^{\circ}$ $\Rightarrow \quad \theta=90^{\circ}-61^{\circ}=29^{\circ} \approx 30^{\circ}$
Apply Snell's law at point $D$,

$\begin{aligned} & \mu_g \sin i_c=\mu_w \sin 90^{\circ} \\ & \Rightarrow \sin i_c=\frac{\mu_w}{\mu_g}=\frac{1.33}{1.52}\end{aligned}$
$\Rightarrow \quad i_c=\sin ^{-1}\left(\frac{1.33}{1.52}\right)=61^{\circ}$
From figure, $\theta+i_c=90^{\circ}$ $\Rightarrow \quad \theta=90^{\circ}-61^{\circ}=29^{\circ} \approx 30^{\circ}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.