Search any question & find its solution
Question:
Answered & Verified by Expert
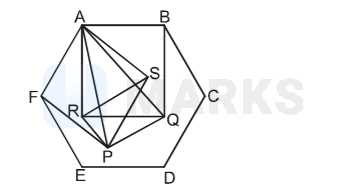
In the figure given below, $\mathrm{ABCDEF}$ is a regular hexagon of side length $1$, $\mathrm{AFPS}$ and $\mathrm{ABQR}$ are squares. Then the ratio Area $\mathrm{(APQ)}/$Area $\mathrm{(SRP)}$ equals
Options:

Solution:
2790 Upvotes
Verified Answer
The correct answer is:
$2$
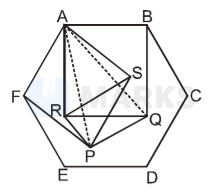
In $\triangle \mathrm{APQ}$
$\mathrm{AP}=\mathrm{AQ}=\sqrt{2}, \angle \mathrm{APQ}=30^{\circ}$
In $\Delta$ $\mathrm{SRP}$
$\mathrm{S R=S P=1}, \angle \mathrm{R S P=30}^{\circ}$
$\angle \mathrm{FAB}=120^{\circ}$
$\angle \mathrm{B A S}=\angle \mathrm{F A B}-\angle \mathrm{F A S}=120^{\circ}-90^{\circ}=30^{\circ}$
$\angle \mathrm{S A R}=\angle \mathrm{B A R}-\angle \mathrm{B A S}=60^{\circ}$
In $\triangle \mathrm{A R S}$
$\begin{array}{l}
\cos 60^{\circ}=\frac{1+1-\mathrm{SR}^{2}}{2.1 .1}[\because \mathrm{AR}=\mathrm{AS}=1] \\
\Rightarrow \mathrm{SR}=1
\end{array}$
Now, $\angle \mathrm{RSP}=\angle \mathrm{ASP}-\angle \mathrm{ASR}$
$=90^{\circ}-60^{\circ}=30^{\circ}[\because$ $\mathrm{ASR}$ is equilateral]
Now, from $\Delta \mathrm{SRP} \Rightarrow \mathrm{RP}=\frac{\sqrt{3}-1}{2 \sqrt{2}}$
In $\triangle \mathrm{APR}$
$\cos \angle \mathrm{RAP}=\frac{(\sqrt{2})^{2}+1^{2}-P R^{2}}{2 \sqrt{2}}$
$\Rightarrow \cos \angle \mathrm{RAP}=15^{\circ}$
$\angle \mathrm{PAQ}=\angle \mathrm{RAQ}-\angle \mathrm{RAP}=45^{\circ}-15^{\circ}=30^{\circ}$
Now, $\frac{\operatorname{ar}(\Delta \mathrm{APQ})}{\operatorname{ar}(\Delta \mathrm{SRP})}=\frac{\frac{1}{2} \times \sqrt{2} \times \sqrt{2} \sin 30^{\circ}}{\frac{1}{2} \times 1 \times 1 \times \sin 30^{\circ}}=2$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.