Search any question & find its solution
Question:
Answered & Verified by Expert
In the figure shown, the blocks have equal masses. Friction, mass of the string and the mass of the pulley are negligible. The magnitude of the acceleration of the centre of mass of the two blocks is (Acceleration due to gravity \(=g\)).
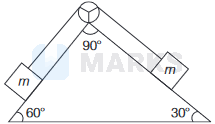
Options:

Solution:
1088 Upvotes
Verified Answer
The correct answer is:
\(\left(\frac{\sqrt{3}-1}{4 \sqrt{2}}\right) g\)
For a pulley and block system on a smooth double inclined plane as shown below
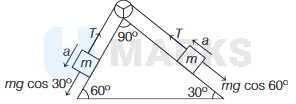
Force equation for both the blocks,
\(\Rightarrow \quad m g \cos 30^{\circ}-T=m a\) ...(i)
\(\Rightarrow \quad T-m g \cos 60^{\circ}=m a\) ...(ii)
From above equation we get,
\(a=\frac{(\sqrt{3}-1)}{4} g\)
\(\because\) Magnitude of the acceleration of centre of mass,
\(\mathbf{a}_{C M}=\left|\frac{m \mathbf{a}_1+m \mathbf{a}_2}{m+m}\right|\)
Here, \(\mathbf{a}_{C M}=\left|\frac{\left(\frac{\sqrt{3}-1}{4}\right) g \hat{\mathbf{i}}+\left(\frac{\sqrt{3}-1}{4}\right) g \hat{\mathbf{j}}}{2}\right|\)
\(\begin{aligned}
& =\frac{g}{2} \sqrt{\left(\frac{\sqrt{3}-1}{4}\right)^2+\left(\frac{\sqrt{3}-1}{4}\right)^2} \\
& =\frac{g}{2} \times \sqrt{2} \times \frac{\sqrt{3}-1}{4} \\
& =\left(\frac{\sqrt{3}-1}{4 \sqrt{2}}\right) g
\end{aligned}\)
Hence, option (d) is correct.

Force equation for both the blocks,
\(\Rightarrow \quad m g \cos 30^{\circ}-T=m a\) ...(i)
\(\Rightarrow \quad T-m g \cos 60^{\circ}=m a\) ...(ii)
From above equation we get,
\(a=\frac{(\sqrt{3}-1)}{4} g\)
\(\because\) Magnitude of the acceleration of centre of mass,
\(\mathbf{a}_{C M}=\left|\frac{m \mathbf{a}_1+m \mathbf{a}_2}{m+m}\right|\)
Here, \(\mathbf{a}_{C M}=\left|\frac{\left(\frac{\sqrt{3}-1}{4}\right) g \hat{\mathbf{i}}+\left(\frac{\sqrt{3}-1}{4}\right) g \hat{\mathbf{j}}}{2}\right|\)
\(\begin{aligned}
& =\frac{g}{2} \sqrt{\left(\frac{\sqrt{3}-1}{4}\right)^2+\left(\frac{\sqrt{3}-1}{4}\right)^2} \\
& =\frac{g}{2} \times \sqrt{2} \times \frac{\sqrt{3}-1}{4} \\
& =\left(\frac{\sqrt{3}-1}{4 \sqrt{2}}\right) g
\end{aligned}\)
Hence, option (d) is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.