Search any question & find its solution
Question:
Answered & Verified by Expert
In the figure shown, the magnetic field induction as the point $\mathrm{O}$ will be
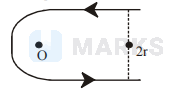
Options:

Solution:
1634 Upvotes
Verified Answer
The correct answer is:
$\frac{\mu_{0} \mathrm{i}}{2 \pi \mathrm{r}}$
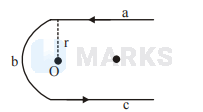
Field due to a straight wire of infinite length is $\frac{\mu_{0} \mathrm{i}}{4 \pi \mathrm{r}}$ ifthe point is on a line perpendicular to its length while at the centre of a semicurcular coil is $\frac{\mu_{0} \pi i}{4 \pi r}$
$$
\begin{array}{l}
\therefore \mathrm{B}=\mathrm{B}_{\mathrm{a}}+\mathrm{B}_{\mathrm{b}}+\mathrm{B}_{\mathrm{c}} \\
=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{i}}{\mathrm{r}}+\frac{\mu_{0}}{4 \pi} \frac{\pi \mathrm{i}}{\mathrm{r}}+\frac{\mu_{0}}{4 \pi \mathrm{r}} \frac{\mathrm{i}}{\mathrm{r}} \\
=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{i}}{\mathrm{r}}(\pi+2) \text { out of the phase }
\end{array}
$$

$$
\begin{array}{l}
\therefore \mathrm{B}=\mathrm{B}_{\mathrm{a}}+\mathrm{B}_{\mathrm{b}}+\mathrm{B}_{\mathrm{c}} \\
=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{i}}{\mathrm{r}}+\frac{\mu_{0}}{4 \pi} \frac{\pi \mathrm{i}}{\mathrm{r}}+\frac{\mu_{0}}{4 \pi \mathrm{r}} \frac{\mathrm{i}}{\mathrm{r}} \\
=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{i}}{\mathrm{r}}(\pi+2) \text { out of the phase }
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.