Search any question & find its solution
Question:
Answered & Verified by Expert
In the following common emitter circuit, if $\beta=100, V_{C E}=-7 \mathrm{~V}, V_{B E}$ is negligible, $R_C=2 \mathrm{k} \Omega$, then $I_B=$ ?
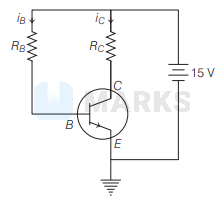
Options:

Solution:
2479 Upvotes
Verified Answer
The correct answer is:
$0.04 \mathrm{~mA}$
$\begin{aligned} & \text { Given that, } V_{C E}=-7 \mathrm{~V}, \beta=100 \\ & \qquad R_C=2 \mathrm{k} \Omega=2000 \Omega, V_{C C}=15 \mathrm{~V}\end{aligned}$
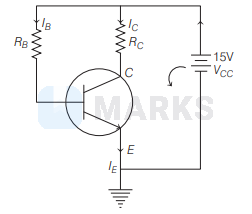
We know that, the current gain in common emitter circuit is
$$
\beta=I_C / I_B...(i)
$$
By KVL in right loop, $V_{C C}-I_C R_C+V_{C E}=0$
Substituting the values, we get
$$
\begin{aligned}
15-I_c(2000)-7 & =0 \\
I_C & =\frac{8}{2000}=4 \mathrm{~mA}...(ii)
\end{aligned}
$$
Putting value of $I_C$ in Eq. (i), we get
$$
\begin{aligned}
& \beta=4 / I_B \Rightarrow 100=4 / I_B \\
& I_B=\frac{4}{100} \mathrm{~mA}=0.04 \mathrm{~mA}
\end{aligned}
$$

We know that, the current gain in common emitter circuit is
$$
\beta=I_C / I_B...(i)
$$
By KVL in right loop, $V_{C C}-I_C R_C+V_{C E}=0$
Substituting the values, we get
$$
\begin{aligned}
15-I_c(2000)-7 & =0 \\
I_C & =\frac{8}{2000}=4 \mathrm{~mA}...(ii)
\end{aligned}
$$
Putting value of $I_C$ in Eq. (i), we get
$$
\begin{aligned}
& \beta=4 / I_B \Rightarrow 100=4 / I_B \\
& I_B=\frac{4}{100} \mathrm{~mA}=0.04 \mathrm{~mA}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.