Search any question & find its solution
Question:
Answered & Verified by Expert
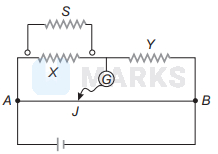
In the meter bridge experiment, the length $A B$ of the wire is $1 \mathrm{~m}$. The resistors $X$ and $Y$ have values $5 \Omega$ and $2 \Omega$ respectively. When a shunt resistance $S$ is connected to $X$, the balancing point is found to be $0.625 \mathrm{~m}$ from $A$. Then, the resistance of the shunt is
Options:

Solution:
1496 Upvotes
Verified Answer
The correct answer is:
$10 \Omega$
Here in given condition, we have
$$
\begin{aligned}
\frac{b x}{\frac{b+x}{2}} & =\frac{0.625}{0.375} \\
\frac{b x}{(b+x) 2} & =\frac{25}{15} \\
\frac{5 b}{(b+5) 2} & =\frac{5}{3} \\
\frac{b}{2 b+10} & =\frac{1}{3} \\
3 b-2 b & =10 \\
b & =10 \Omega
\end{aligned}
$$
$$
\begin{aligned}
\frac{b x}{\frac{b+x}{2}} & =\frac{0.625}{0.375} \\
\frac{b x}{(b+x) 2} & =\frac{25}{15} \\
\frac{5 b}{(b+5) 2} & =\frac{5}{3} \\
\frac{b}{2 b+10} & =\frac{1}{3} \\
3 b-2 b & =10 \\
b & =10 \Omega
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.