Search any question & find its solution
Question:
Answered & Verified by Expert
In the pulley system, the mass of ball is 1.2 times greater than the mass of the rod. The length of the rod is $50 \mathrm{~cm}$. The ball is set on the same level as the lower end of the rod and then released. What is the acceleration of the rod with which it comes down? Assume the pulleys and threads are massless and friction force is neglected. (Use, $g=10 \mathrm{~m} / \mathrm{s}^2$ )
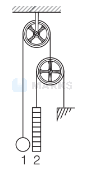
Options:

Solution:
2742 Upvotes
Verified Answer
The correct answer is:
$3 \mathrm{~m} / \mathrm{s}^2$
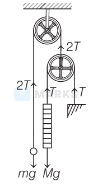
The free body diagram for given system is as
shown below
For ball,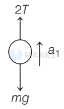
$\Rightarrow \quad m a_1=2 T-m g$
For rod,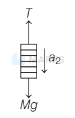
$\Rightarrow \quad M a_2=M g-T$
As, thread is uniform and of constant length, so $2 a_1=a_2$
From Eq. (i), we get
$\frac{m a_2}{2}=2 T-m g$
Multiplying Eq. (ii) by 2 and adding to Eq. (iii), we get
$\begin{gathered}2 M a_2+\frac{m a_2}{2}=2 M g-m g \\ \Rightarrow \quad a_2=\frac{(2 M-m)}{\left(2 M+\frac{m}{2}\right)} g=\frac{\left(2-\frac{m}{M}\right)}{\left(2+\frac{m}{2 M}\right)} g\end{gathered}$
Here, $\frac{m}{M}=1.2$ and $g=10 \mathrm{~ms}^{-2}$
$\begin{aligned} \therefore \quad a_2 & =\frac{(2-1.2)}{\left(2+\frac{1.2}{2}\right)} \times 10 \\ & =\frac{0.8}{26} \times 10=\frac{40}{1.3}=3 \mathrm{~m} / \mathrm{s}^2\end{aligned}$
shown below

For ball,

$\Rightarrow \quad m a_1=2 T-m g$
For rod,

$\Rightarrow \quad M a_2=M g-T$
As, thread is uniform and of constant length, so $2 a_1=a_2$
From Eq. (i), we get
$\frac{m a_2}{2}=2 T-m g$
Multiplying Eq. (ii) by 2 and adding to Eq. (iii), we get
$\begin{gathered}2 M a_2+\frac{m a_2}{2}=2 M g-m g \\ \Rightarrow \quad a_2=\frac{(2 M-m)}{\left(2 M+\frac{m}{2}\right)} g=\frac{\left(2-\frac{m}{M}\right)}{\left(2+\frac{m}{2 M}\right)} g\end{gathered}$
Here, $\frac{m}{M}=1.2$ and $g=10 \mathrm{~ms}^{-2}$
$\begin{aligned} \therefore \quad a_2 & =\frac{(2-1.2)}{\left(2+\frac{1.2}{2}\right)} \times 10 \\ & =\frac{0.8}{26} \times 10=\frac{40}{1.3}=3 \mathrm{~m} / \mathrm{s}^2\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.