Search any question & find its solution
Question:
Answered & Verified by Expert
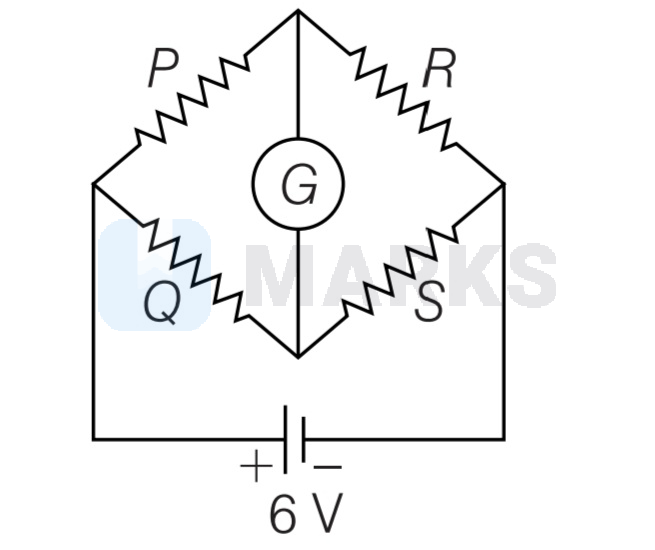
In the Wheatstone's network given, $P=10 \Omega$, $Q=20 \Omega, R=15 \Omega, S=30 \Omega$ the current have passing through the battery (of negligible internal resistance) is
Options:

Solution:
1422 Upvotes
Verified Answer
The correct answer is:
$0.36 \mathrm{~A}$
The balanced condition for Wheatstones bridge is
$$
\frac{P}{Q}=\frac{R}{S}
$$
as is obvious from the given values.
No, current flows through galvanometer is zero.
Now, $P$ and $R$ are in series, so
Resistance $R_{1}=P+R=10+15=25 \Omega$
Similarly, $Q$ and $S$ are in series, so
Resistance $R_{2}=R+S=20+30=50 \Omega$
Net resistance of the network as $R_{1}$ and $R_{2}$ are in parallel
$$
\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}
$$
$$
\begin{array}{ll}
\therefore & R=\frac{25 \times 50}{25+50}=\frac{50}{3} \Omega \\
\text { Hence, } & I=\frac{V}{R}=\frac{6}{50}=0.36 \mathrm{~A}
\end{array}
$$
$$
\frac{P}{Q}=\frac{R}{S}
$$
as is obvious from the given values.
No, current flows through galvanometer is zero.
Now, $P$ and $R$ are in series, so
Resistance $R_{1}=P+R=10+15=25 \Omega$
Similarly, $Q$ and $S$ are in series, so
Resistance $R_{2}=R+S=20+30=50 \Omega$
Net resistance of the network as $R_{1}$ and $R_{2}$ are in parallel
$$
\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}
$$
$$
\begin{array}{ll}
\therefore & R=\frac{25 \times 50}{25+50}=\frac{50}{3} \Omega \\
\text { Hence, } & I=\frac{V}{R}=\frac{6}{50}=0.36 \mathrm{~A}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.