Search any question & find its solution
Question:
Answered & Verified by Expert
In Young's double slit experiment, the $10^{\text {th }}$ maximum of wavelength $\lambda_1$ is at a distance of $y_1$ from the central maximum. When the wavelength of the source is changed to $\lambda_2, 5^{\text {th }}$ maximum is at a distance of $y_2$ from its central maximum. The ratio $\left(\frac{y_1}{y_2}\right)$ is
Options:
Solution:
1964 Upvotes
Verified Answer
The correct answer is:
$\frac{2 \lambda_2}{\lambda_1}$
Position fringe from central maxima
$y_1=\frac{n \lambda_1 D}{d}$
Given,
$n=10$
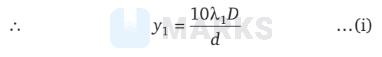
For second source
$\therefore \quad \frac{y_1}{y_2}=\frac{\frac{10 \lambda_1 D}{d}}{\frac{5 \lambda_2 D}{d}}$
$\Rightarrow \quad \frac{y_1}{y_2}=\frac{2 \lambda_1}{\lambda_2}$
$y_1=\frac{n \lambda_1 D}{d}$
Given,
$n=10$
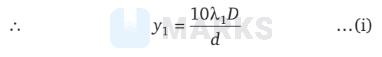
For second source

$\therefore \quad \frac{y_1}{y_2}=\frac{\frac{10 \lambda_1 D}{d}}{\frac{5 \lambda_2 D}{d}}$
$\Rightarrow \quad \frac{y_1}{y_2}=\frac{2 \lambda_1}{\lambda_2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.