Search any question & find its solution
Question:
Answered & Verified by Expert
Let $A(1,1), B(1,-1), C(-1,1)$ be the vertices of $\triangle A B C$. Let $S$ be the circum-centre, $O$ be the orthocentre and $I$ be the incentre of the $\triangle A B C$. Then $I S+O S=$
Options:
Solution:
1341 Upvotes
Verified Answer
The correct answer is:
$2$
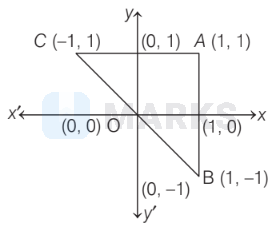
It is clear that $\triangle A B C$ is a right angled triangle at $A$. $\therefore$ Circum-centre, $S=$ Mid-point of hypotenuse $B C$
$=\left(\frac{-1+1}{2}, \frac{1-1}{2}\right)=(0,0)$
Orthocentre, $O=$ Coordinate of vertice at which right angle is there
$=A=(1,1)$
and Incentre
$\begin{aligned} & I=\left(\begin{array}{c}\frac{2 \sqrt{2} \times 1+2 \times 1+2 \times(-1)}{2 \sqrt{2}+2+2}, \\ \frac{2 \sqrt{2} \times 1+2 \times 1+2 \times-1}{2 \sqrt{2}+2+2}\end{array}\right) \\ & =\left(\frac{2 \sqrt{2}}{2 \sqrt{2}+4}, \frac{2 \sqrt{2}}{2 \sqrt{2}+4}\right)=(\sqrt{2}-1, \sqrt{2}-1) \\ & \text { IS }+ \text { OS }=\sqrt{(\sqrt{2}-1)^2+(\sqrt{2}-1)^2}+\sqrt{(1)^2+(1)^2} \\ & =\sqrt{2}(\sqrt{2}-1)+\sqrt{2}=2-\sqrt{2}+\sqrt{2}=2\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.