Search any question & find its solution
Question:
Answered & Verified by Expert
Let $A=\{1,2,3, \ldots .14\}$. Define a relation $R$ from $A$ to $A$ by $R=\{(x, y): 3 x-y=0$ where $x, y \in A\}$. Write down the domain, co-domain and range.
Solution:
1072 Upvotes
Verified Answer
(i) By the definition of the relation, $R=\{(1,3)(2,6)$, $(3,9),(4,12)\}$. The corresponding arrow diagram is:
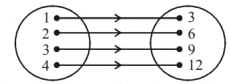
(ii) We can see that the set of first element i.e., the domain $=\{1,2,3,4\}$.
Similarly, the set of second elements (images) i.e., the range $=\{3,6,9,12\}$ and the co-domain $=\{1,2,3, \ldots .14\}$.

(ii) We can see that the set of first element i.e., the domain $=\{1,2,3,4\}$.
Similarly, the set of second elements (images) i.e., the range $=\{3,6,9,12\}$ and the co-domain $=\{1,2,3, \ldots .14\}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.