Search any question & find its solution
Question:
Answered & Verified by Expert
Let $\mathbf{A}_1+\mathbf{A}_2=5 \mathbf{A}_3, \mathbf{A}_1-\mathbf{A}_2=3 \mathbf{A}_3$, $\mathbf{A}_3=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}$, then $\frac{\left|\mathbf{A}_1\right|}{\left|\mathbf{A}_2\right|} \mathrm{i}$
Options:
Solution:
2769 Upvotes
Verified Answer
The correct answer is:
4
Given that,
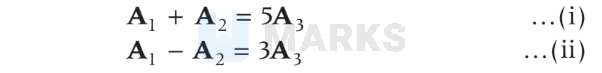
On adding Eqs. (i) and (ii), we get
$\begin{aligned}
2 \mathbf{A}_1 & =8 \mathbf{A}_3 \Rightarrow \mathbf{A}_1=4 \mathbf{A}_3 \\
\mathbf{A}_1 & =4(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}})\left[\because \mathbf{A}_3=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \text { (given) }\right] \\
\mathbf{A}_1 & =8 \hat{\mathbf{i}}+16 \hat{\mathbf{j}}
\end{aligned}$
On subtracting Eqs. (ii) from (i), we get
$\begin{aligned}
2 \mathbf{A}_2 & =2 \mathbf{A}_3 \Rightarrow \mathbf{A}_2=\mathbf{A}_3=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \\
\frac{\left|\mathbf{A}_1\right|}{\left|\mathbf{A}_2\right|} & =\frac{|8 \hat{\mathbf{i}}+16 \hat{\mathbf{j}}|}{|2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}|}=\frac{\sqrt{(8)^2+(16)^2}}{(2)^2+(4)^2} \\
& =\frac{\sqrt{64+256}}{\sqrt{4+16}}=\frac{\sqrt{320}}{\sqrt{20}}=\sqrt{16}=4
\end{aligned}$
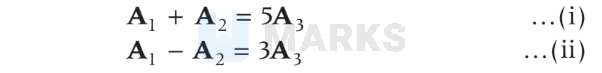
On adding Eqs. (i) and (ii), we get
$\begin{aligned}
2 \mathbf{A}_1 & =8 \mathbf{A}_3 \Rightarrow \mathbf{A}_1=4 \mathbf{A}_3 \\
\mathbf{A}_1 & =4(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}})\left[\because \mathbf{A}_3=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \text { (given) }\right] \\
\mathbf{A}_1 & =8 \hat{\mathbf{i}}+16 \hat{\mathbf{j}}
\end{aligned}$
On subtracting Eqs. (ii) from (i), we get
$\begin{aligned}
2 \mathbf{A}_2 & =2 \mathbf{A}_3 \Rightarrow \mathbf{A}_2=\mathbf{A}_3=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \\
\frac{\left|\mathbf{A}_1\right|}{\left|\mathbf{A}_2\right|} & =\frac{|8 \hat{\mathbf{i}}+16 \hat{\mathbf{j}}|}{|2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}|}=\frac{\sqrt{(8)^2+(16)^2}}{(2)^2+(4)^2} \\
& =\frac{\sqrt{64+256}}{\sqrt{4+16}}=\frac{\sqrt{320}}{\sqrt{20}}=\sqrt{16}=4
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.