Search any question & find its solution
Question:
Answered & Verified by Expert
Let $A_{1}, A_{2}, A_{3}$ be regions in the $x y$-plane defined by
$$
\begin{array}{l}
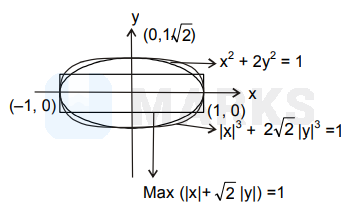
A_{1}=\left\{(x, y): x^{2}+2 y^{2} \leq 1\right\} \\
A_{2}=\left\{(x, y):|x|^{3}+2 \sqrt{2}|y|^{3} \leq 1\right\}
\end{array}
$$
$A_{3}=\{(x, y): \max (|x|, \sqrt{2}|y|) \leq 1$. Then
Options:
$$
\begin{array}{l}
A_{1}=\left\{(x, y): x^{2}+2 y^{2} \leq 1\right\} \\
A_{2}=\left\{(x, y):|x|^{3}+2 \sqrt{2}|y|^{3} \leq 1\right\}
\end{array}
$$
$A_{3}=\{(x, y): \max (|x|, \sqrt{2}|y|) \leq 1$. Then
Solution:
2432 Upvotes
Verified Answer
The correct answer is:
$A_{3} \supset A_{2} \supset A_{1}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.