Search any question & find its solution
Question:
Answered & Verified by Expert
Let $A$ and $B$ be two distinct points on the parabola $y^2=4 x$. If the axis of the parabola touches a circle of radius $r$ having $A B$ as its diameter, then the slope of the line joining $A$ and $B$ can be
Options:
Solution:
2553 Upvotes
Verified Answer
The correct answers are:
$\frac{2}{r}$
,
$-\frac{2}{r}$
$\frac{2}{r}$
,
$-\frac{2}{r}$
Here, coordinate $M=\left(\frac{t_1^2+t_2^2}{2}, t_1+t_2\right) i e$, mid point of chord $A B$.
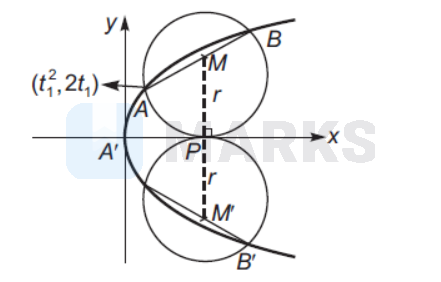
$M P=t_1+t_2=r$ Also, $\quad m_{A B}=\frac{2 t_2-2 t_1}{t_2^2-t_1^2}=\frac{2^{\ldots(i)}}{t_2+t_1}$ (when $A B$ is chord)
$$
\Rightarrow \quad m_{A B}=\frac{2}{r}
$$
[from Eq. (i)]
Also, $\quad m_{A^{\prime} B^{\prime}}=-\frac{2}{r}$ (when $A^{\prime} B^{\prime}$ is chord)
Hence, (c, d) is the correct option.

$M P=t_1+t_2=r$ Also, $\quad m_{A B}=\frac{2 t_2-2 t_1}{t_2^2-t_1^2}=\frac{2^{\ldots(i)}}{t_2+t_1}$ (when $A B$ is chord)
$$
\Rightarrow \quad m_{A B}=\frac{2}{r}
$$
[from Eq. (i)]
Also, $\quad m_{A^{\prime} B^{\prime}}=-\frac{2}{r}$ (when $A^{\prime} B^{\prime}$ is chord)
Hence, (c, d) is the correct option.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.