Search any question & find its solution
Question:
Answered & Verified by Expert
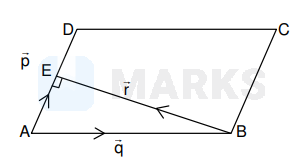
Let $A B C D$ be a parallelogram such that $\overrightarrow{A B}=\overrightarrow{\mathrm{q}}, \overrightarrow{A D}=\vec{p}$ and $\angle B A D$ be an acute angle. If $\vec{r}$ is the vector that coincides with the altitude directed from the vertex $B$ to the side $A D$, then $\vec{r}$ is given by
Options:
Solution:
2791 Upvotes
Verified Answer
The correct answer is:
$\vec{r}=-\overrightarrow{\mathrm{q}}+\left(\frac{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}}{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}}}\right) \overrightarrow{\mathrm{p}}$
$\vec{r}=-\overrightarrow{\mathrm{q}}+\left(\frac{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}}{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}}}\right) \overrightarrow{\mathrm{p}}$
$\overrightarrow{\mathrm{AE}}=$ vector component of $\overrightarrow{\mathrm{q}}$ on $\overrightarrow{\mathrm{p}}$
$\overrightarrow{\mathrm{AE}}=\frac{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})} \overrightarrow{\mathrm{p}} \quad \therefore$ From $\triangle \mathrm{ABE} ; \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BE}}=\overrightarrow{\mathrm{AE}}$
$\Rightarrow \overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}}=\frac{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}) \overrightarrow{\mathrm{p}}}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})} \quad \Rightarrow \overrightarrow{\mathrm{r}}=-\overrightarrow{\mathrm{q}}+\frac{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}})} \overrightarrow{\mathrm{p}}$
$\overrightarrow{\mathrm{AE}}=\frac{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})} \overrightarrow{\mathrm{p}} \quad \therefore$ From $\triangle \mathrm{ABE} ; \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BE}}=\overrightarrow{\mathrm{AE}}$
$\Rightarrow \overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}}=\frac{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}) \overrightarrow{\mathrm{p}}}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})} \quad \Rightarrow \overrightarrow{\mathrm{r}}=-\overrightarrow{\mathrm{q}}+\frac{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}})}{(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{p}})} \overrightarrow{\mathrm{p}}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.