Search any question & find its solution
Question:
Answered & Verified by Expert
Let $A D$ and $B C$ be two vertical poles at $A$ and $B$ respectively on a horizontal ground. If $A D=8 \mathrm{~m}, B C=11 \mathrm{~m}$ and $A B=10 \mathrm{~m}$, then the distance (in meters) of point $M$ on $A B$ from the point $A$ such that $M D^2+M C^2$ is minimum, is
Options:
Solution:
2554 Upvotes
Verified Answer
The correct answer is:
5
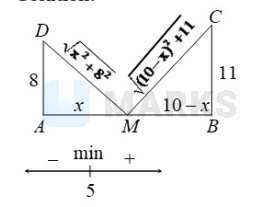
$\begin{aligned} & f(x)=M D^2+M C^2 \\ & \Rightarrow f(x)=x^2+8^2+(10-x)^2+11^2 \\ & \Rightarrow f^{\prime}(x)=2 x-2(10-x) \\ & \Rightarrow f^{\prime}(x)=4 x-20 \\ & \text { for } f(x) \text { to be minimum } x=5\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.