Search any question & find its solution
Question:
Answered & Verified by Expert
Let $\mathrm{ABC}$ be a triangle with vertices at points $\mathrm{A}$ $(2,3,5)$, B $(-1,3,2)$ and $\mathrm{C}(\lambda, 5, \mu)$ in three dimensional space. If the median through $\mathrm{A}$ is equally inclined with the axes, then $(\lambda, \mu)$ is equal to:
Options:
Solution:
2622 Upvotes
Verified Answer
The correct answer is:
$(7,10)$
$(7,10)$
Since $\mathrm{AD}$ is the median
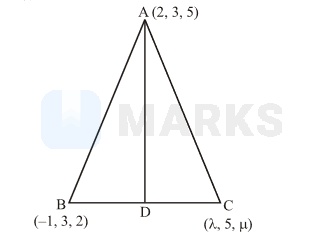
$$
\therefore \quad \mathrm{D}=\left(\frac{\lambda-1}{2}, 4, \frac{\mu+2}{2}\right)
$$
Now, dR's of AD is
$$
a=\left(\frac{\lambda-1}{2}-2\right)=\frac{\lambda-5}{2}
$$
$$
b=4-3=1, c=\frac{\mu+2}{2}-5=\frac{\mu-8}{2}
$$
Also, $a, b, c$ are $\mathrm{dR}$ 's
$\therefore a=k l, b=k m, c=k n$ where $l=m=n$ and $l^2+m^2+n^2=1$
$$
\Rightarrow l=m=n=\frac{1}{\sqrt{3}}
$$
Now, $a=1, b=1$ and $c=1$
$\Rightarrow \lambda=7$ and $\mu=10$

$$
\therefore \quad \mathrm{D}=\left(\frac{\lambda-1}{2}, 4, \frac{\mu+2}{2}\right)
$$
Now, dR's of AD is
$$
a=\left(\frac{\lambda-1}{2}-2\right)=\frac{\lambda-5}{2}
$$
$$
b=4-3=1, c=\frac{\mu+2}{2}-5=\frac{\mu-8}{2}
$$
Also, $a, b, c$ are $\mathrm{dR}$ 's
$\therefore a=k l, b=k m, c=k n$ where $l=m=n$ and $l^2+m^2+n^2=1$
$$
\Rightarrow l=m=n=\frac{1}{\sqrt{3}}
$$
Now, $a=1, b=1$ and $c=1$
$\Rightarrow \lambda=7$ and $\mu=10$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.