Search any question & find its solution
Question:
Answered & Verified by Expert
Let $\mathrm{ABC}$ be an equilateral triangle, let KLMN be a rectangle with $\mathrm{K}, \mathrm{L}$ on $\mathrm{BC}, \mathrm{M}$ on $\mathrm{AC}$ and $\mathrm{N}$ on $\mathrm{AB}$. Suppose AN $/ \mathrm{NB}=2$ and the area of triangle BKN is $6 .$ The area of the triangle $\mathrm{ABC}$ is-
Options:
Solution:
2372 Upvotes
Verified Answer
The correct answer is:
108
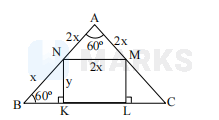
$y=\frac{\sqrt{3} x}{2}$
$z=\frac{x}{2}$
$\frac{1}{2} y z=6 \Rightarrow x^{2}=\frac{48}{\sqrt{3}}$
Area of $\Delta \mathrm{ABC}=6+6+2 \mathrm{xy}+\frac{1}{2}(2 \mathrm{x})(2 \mathrm{x}) \sin 60^{\circ}$
$$
=12+2 \mathrm{x} \frac{\sqrt{3} \mathrm{x}}{2}+2 \mathrm{x}^{2} \frac{\sqrt{3}}{2}
$$
$$
12+2 \sqrt{3} \times \frac{48}{\sqrt{3}}=108
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.