Search any question & find its solution
Question:
Answered & Verified by Expert
Let be defined as for all where such that and for the maximum value of is If then the least value of is equal to
Solution:
2909 Upvotes
Verified Answer
The correct answer is:
5
Given and
and
Given the maximum value of
From the equations and we get and
We know that, the vertex of the quadratic is at
Thus, the vertex of is at hence both the numbers are on the same side of the vertex and the graph of is given below.
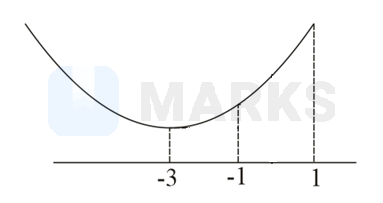
For, we have
Least value of is
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.