Search any question & find its solution
Question:
Answered & Verified by Expert
Let $f(x)$ and $g(x)$ be twice differentiable functions such that $f(x)=x^2+g^{\prime}(1) x+g^{\prime \prime}(2)$ and $g(x)=f(\mathrm{l}) x^2+x f^{\prime}(x)+f^{\prime \prime}(x)$. Then $f(x)-g(x)=$
Options:
Solution:
1262 Upvotes
Verified Answer
The correct answer is:
$x^2-2$
We have,
$f(x)=x^2+x g^{\prime}(1)+g^{\prime \prime}(2)$
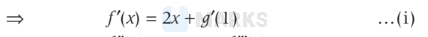
$\Rightarrow \quad f^{\prime \prime}(x)=2 \Rightarrow f^{\prime \prime \prime \prime}(x)=0$
Again,
$\begin{array}{ll}
& g(x)=f(\mathrm{l}) x^2+x f^{\prime}(x)+f^{\prime \prime}(x) \\
\Rightarrow \quad & g^{\prime}(x)=2 x f(1)+f^{\prime}(x)+x f^{\prime \prime \prime}(x)+f^{\prime \prime \prime}(x) \\
\text { Put } x=1 &
\end{array}$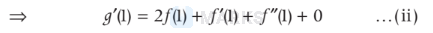
Put $x=1$ in Eq. (i), we get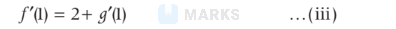
From Eq. (ii) and Eq. (iii), we get
$g^{\prime}(\mathrm{l})=2 f(\mathrm{l})+2+g^{\prime}(\mathrm{l})+2$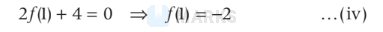
Now, again,
$\begin{aligned}
g^{\prime \prime}(x) & =2 f(1)+f^{\prime \prime}(x)+f^{\prime \prime}(x)+x f^{\prime \prime \prime}(x) \\
& =2 f(1)+4=-4+4 \\
g^{\prime \prime}(x) & =0 \\
\therefore \quad \quad \quad f(x) & =x^2+x g^{\prime}(1)+g^{\prime \prime}(2)=x^2+x g^{\prime}(1)
\end{aligned}$
Put, $x=1$
$f(1)=1+g^{\prime}(1) \Rightarrow-2=1+g^{\prime}(1)$
$\begin{aligned} & \Rightarrow \quad g^{\prime}(1)=-3 \\ & \therefore \quad f(x)=x^2+x(-3)=x^2-3 x \\ & \therefore \quad g(x)=f(1) x^2+x f^{\prime}(x)+f^{\prime \prime}(x) \\ & =-2 x^2+x(2 x-3)+2 \\ & =-2 x^2+2 x^2-3 x+2=2-3 x \\ & \therefore \quad f(x)-g(x)=x^2-3 x-2+3 x=x^2-2 \\ & \end{aligned}$
$f(x)=x^2+x g^{\prime}(1)+g^{\prime \prime}(2)$
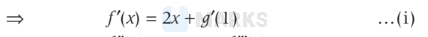
$\Rightarrow \quad f^{\prime \prime}(x)=2 \Rightarrow f^{\prime \prime \prime \prime}(x)=0$
Again,
$\begin{array}{ll}
& g(x)=f(\mathrm{l}) x^2+x f^{\prime}(x)+f^{\prime \prime}(x) \\
\Rightarrow \quad & g^{\prime}(x)=2 x f(1)+f^{\prime}(x)+x f^{\prime \prime \prime}(x)+f^{\prime \prime \prime}(x) \\
\text { Put } x=1 &
\end{array}$
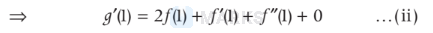
Put $x=1$ in Eq. (i), we get
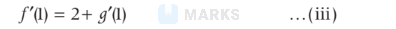
From Eq. (ii) and Eq. (iii), we get
$g^{\prime}(\mathrm{l})=2 f(\mathrm{l})+2+g^{\prime}(\mathrm{l})+2$
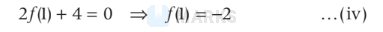
Now, again,
$\begin{aligned}
g^{\prime \prime}(x) & =2 f(1)+f^{\prime \prime}(x)+f^{\prime \prime}(x)+x f^{\prime \prime \prime}(x) \\
& =2 f(1)+4=-4+4 \\
g^{\prime \prime}(x) & =0 \\
\therefore \quad \quad \quad f(x) & =x^2+x g^{\prime}(1)+g^{\prime \prime}(2)=x^2+x g^{\prime}(1)
\end{aligned}$
Put, $x=1$
$f(1)=1+g^{\prime}(1) \Rightarrow-2=1+g^{\prime}(1)$
$\begin{aligned} & \Rightarrow \quad g^{\prime}(1)=-3 \\ & \therefore \quad f(x)=x^2+x(-3)=x^2-3 x \\ & \therefore \quad g(x)=f(1) x^2+x f^{\prime}(x)+f^{\prime \prime}(x) \\ & =-2 x^2+x(2 x-3)+2 \\ & =-2 x^2+2 x^2-3 x+2=2-3 x \\ & \therefore \quad f(x)-g(x)=x^2-3 x-2+3 x=x^2-2 \\ & \end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.