Search any question & find its solution
Question:
Answered & Verified by Expert
Let $f(x)=$ Maximum $\left\{x^{2},(1-x)^{2}, 2 x(1-x)\right\}$, where $0 \leq x \leq 1$. Determine the area of the region bounded by the curves $y=f(x), x$-axis, $x=0 \& x=1$
Options:
Solution:
1325 Upvotes
Verified Answer
The correct answer is:
$\frac{17}{27}$
$$
f(x)=\operatorname{Max}\left\{x^{2},(1-x)^{2}, 2 x(1-x)\right\}
$$
coordinate of $A,(1-x)^{2}=2 x(1-x)$
$(1-x)(1-x-2 x)=0$
$x=\frac{1}{3}, A\left(\frac{1}{3}, 0\right)$ coordinate of $B$
$2 x(1-x)=x^{2}, 2(1-x)=x, 2-3 x=0, x=\frac{2}{3}$
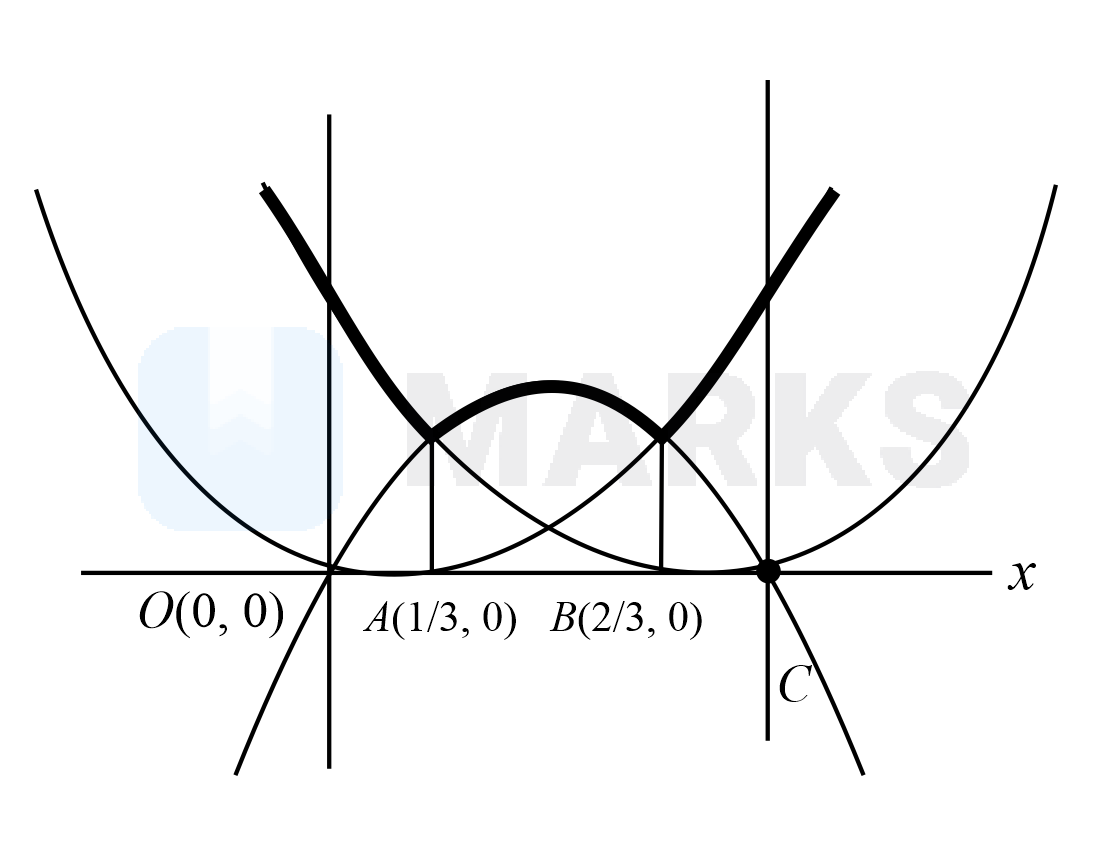
$B\left(\frac{2}{3}, 0\right)$ Req. Area $=\int_{0}^{1 / 3}(1-x)^{2} d x+\int_{1 / 3}^{2 / 3} 2 x(1-x) d x+\int_{\frac{2}{3}}^{1} x^{2} d x$
$=\frac{17}{27}$
f(x)=\operatorname{Max}\left\{x^{2},(1-x)^{2}, 2 x(1-x)\right\}
$$
coordinate of $A,(1-x)^{2}=2 x(1-x)$
$(1-x)(1-x-2 x)=0$
$x=\frac{1}{3}, A\left(\frac{1}{3}, 0\right)$ coordinate of $B$
$2 x(1-x)=x^{2}, 2(1-x)=x, 2-3 x=0, x=\frac{2}{3}$

$B\left(\frac{2}{3}, 0\right)$ Req. Area $=\int_{0}^{1 / 3}(1-x)^{2} d x+\int_{1 / 3}^{2 / 3} 2 x(1-x) d x+\int_{\frac{2}{3}}^{1} x^{2} d x$
$=\frac{17}{27}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.