Search any question & find its solution
Question:
Answered & Verified by Expert
Let $f^{\prime}(x)=|x|$ and $g(x)=|x|+a,(a>0)$. For $0 \leq x \leq b$, $\{(x, y) / g(x) \leq y \leq f(x)\}$ represents all the points in the interior of
Options:
Solution:
1847 Upvotes
Verified Answer
The correct answer is:
a parallelogram
Given functions are
$\begin{aligned} & f(x)=|x| \\ & g(x)=|x|+a \quad(a>0) \\ & \text { For } 0 \leq x \leq b,\{(x, y) \mid g(x) \leq y \leq f(x)\}\end{aligned}$
Let us draw the above region
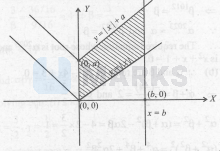
The required region represents all the points in the interior of a parallelogram.
$\begin{aligned} & f(x)=|x| \\ & g(x)=|x|+a \quad(a>0) \\ & \text { For } 0 \leq x \leq b,\{(x, y) \mid g(x) \leq y \leq f(x)\}\end{aligned}$
Let us draw the above region

The required region represents all the points in the interior of a parallelogram.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.