Search any question & find its solution
Question:
Answered & Verified by Expert
Let $\mathrm{P}$ be a point inside a triangle $\mathrm{ABC}$ with $\angle \mathrm{ABC}=90^{\circ}$. Let $\mathrm{P}_{1}$ and $\mathrm{P}_{2}$ be the images of $\mathrm{P}$ under reflection in $\mathrm{AB}$ and $\mathrm{BC}$ respectively. The distance between the circumcenters of triangles $\mathrm{ABC}$ and $\mathrm{P}_{1} \mathrm{P} \mathrm{P}_{2}$ is
Options:
Solution:
2480 Upvotes
Verified Answer
The correct answer is:
$\frac{\mathrm{AC}}{2}$
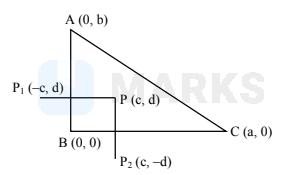
$\mathrm{M}$ is circumcentre of $\triangle \mathrm{ABC}$
$\Rightarrow \mathrm{M}\left(\frac{\mathrm{a}}{2}, \frac{\mathrm{b}}{2}\right)$
$\& \mathrm{~N}$ is circumcentre of $\triangle \mathrm{ABC}$ $\mathrm{N}=(0,0)=\mathrm{B}\left(\right.$ Mid-point of $\left.\mathrm{P}_{1}, \& \mathrm{P}_{2}\right)$
So $\mathrm{MN}=\frac{\mathrm{AC}}{2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.