Search any question & find its solution
Question:
Answered & Verified by Expert
Let $\mathrm{P}(\alpha, \beta, \gamma)$ be the image of the point $\mathrm{Q}(1,6,4)$ in the line $\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}$. Then $2 \alpha+\beta+\gamma$ is equal to_______
Solution:
2186 Upvotes
Verified Answer
The correct answer is:
11
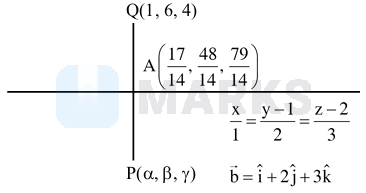
$\begin{aligned} & \mathrm{A}(\mathrm{t}, 2 \mathrm{t}+1,3 \mathrm{t}+2) \\ & \overrightarrow{\mathrm{QA}}=(\mathrm{t}-1) \hat{\mathrm{i}}+(2 \mathrm{t}-5) \hat{\mathrm{j}}+(3 \mathrm{t}-2) \hat{\mathrm{k}} \\ & \overrightarrow{\mathrm{QA}} \cdot \overrightarrow{\mathrm{b}}=0 \\ & (\mathrm{t}-1)+2(2 \mathrm{t}-5)+3(3 \mathrm{t}-2)=0 \\ & 14 \mathrm{t}=17 \\ & \alpha=\frac{20}{14} \quad \beta=\frac{12}{14} \quad \gamma=\frac{102}{14} \\ & 2 \alpha+\beta+\gamma=\frac{154}{14}=11\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.