Search any question & find its solution
Question:
Answered & Verified by Expert
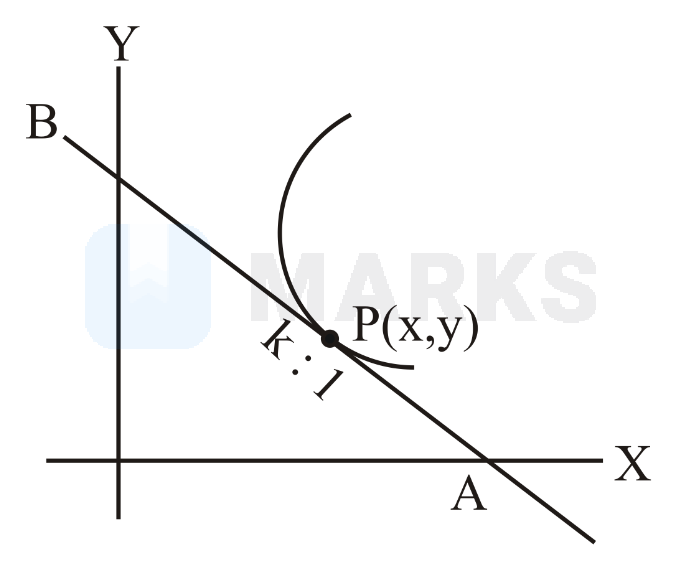
Let the tangent at any point on a curve passing through the points and , intersect positive -axis and -axis at the points and respectively. If and is the solution of the differential equation , then is equal to _______________
Solution:
1895 Upvotes
Verified Answer
The correct answer is:
5
Given,
The tangent at any point on a curve passing through the points and , intersect positive -axis and -axis at the points and respectively,
And and is the solution of the differential equation ,
Now on plotting the diagram we get,
Equation of tangent at is :
Coordinate of
Coordinate of
So,
Now integrating both side, we get
Now given equation passes through and
So, and
Now putting the value of , we get
Integrating the above equation we get,
And the above equation passes through
So,
Hence,
Note: This question was bonus in Jee Mains 2023 April session.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.