Given,

The tangent at any point $\mathrm{P}$ on a curve passing through the points $\left(1,1\right)$ and $\left(\frac{1}{10},100\right)$, intersect positive $\mathrm{x}$-axis and $\mathrm{y}$-axis at the points $\mathrm{A}$ and $\mathrm{B}$ respectively,

And  $P A: P B=1: k$ and $y=y\left(x\right)$ is the solution of the differential equation $e^{\frac{dy}{dx}}=kx+\frac{k}{2},y\left(0\right)=k$,

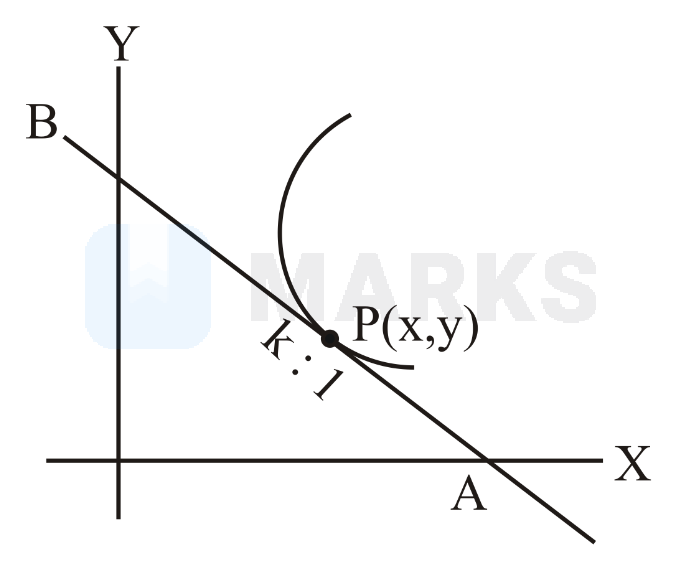
Now on plotting the diagram we get,

Equation of tangent at $P\left(x, y\right)$ is :

$\mathrm{Y}-\mathrm{y}=\frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{X}-\mathrm{x}\right)$

Coordinate of $A=\left(x-y\frac{dx}{dy},0\right)$

Coordinate of $B=\left(0,y-x\frac{dy}{dx}\right)$

$\therefore \left(x,y\right)=\left(\frac{kx-ky\frac{dx}{dy}}{k+1},\frac{y-x\frac{dy}{dx}}{k+1}\right)$

So, $y=\frac{y-x\frac{dy}{dx}}{k+1}$

$\Rightarrow y\left(k+1\right)=y-x\frac{dy}{dx}$

$\Rightarrow ky=-x\frac{dy}{dx}$

$\Rightarrow k\frac{dx}{x}=-\frac{dy}{y}$

Now integrating both side, we get

$k\ln \left|x\right|+\ln \left|y\right|=\ln C ......\left(i\right)$

Now given equation $\left(i\right)$ passes through $\left(1, 1\right)$ and $\left(\frac{1}{10},100\right)$

So, $C = 1$ and $k = 2$

Now putting the value of $k$, we get

$e^{\frac{dy}{dx}}=kx+\frac{k}{2}$

$\Rightarrow e^{\frac{dy}{dx}}=2x+1 \left\{\text{as} k=2\right\}$

$\Rightarrow \frac{dy}{dx}=\ln \left(2x+1\right)$

Integrating the above equation we get,

$y=\frac{1}{2}\left(2x+1\right)\left(\ln \left|2x+1\right|-1\right)+C$

And the above equation passes through $\left(0, 2\right)$

$\Rightarrow C=\frac{5}{2}$

So, $2y=\left(2x+1\right)\left(\ln \left|2x+1\right|-1\right)+5$

$\Rightarrow 2y\left(1\right)=3\left(\ln 3-1\right)+5$

$\Rightarrow 2y\left(1\right)=3\ln \left(3\right)+2$

Hence, $4y\left(1\right)-5{\log }_{\mathrm{e}}3=2\left[3\ln 3+2\right]-5\ln 3$

$\Rightarrow 4y\left(1\right)-5{\log }_{\mathrm{e}}3=6\ln 3+4-5\ln 3$

$\Rightarrow 4y\left(1\right)-5{\log }_{\mathrm{e}}3=4+\ln 3\approx 5$

Note: This question was bonus in Jee Mains 2023 April session.