Search any question & find its solution
Question:
Answered & Verified by Expert
Match the statements of Column I with these in Column II.
[Note : Here $z$ takes values in the complex plane and $\operatorname{Im}(z)$ and $\operatorname{Re}(z)$ denote respectively, the imaginary part and the real part of $z$ ]
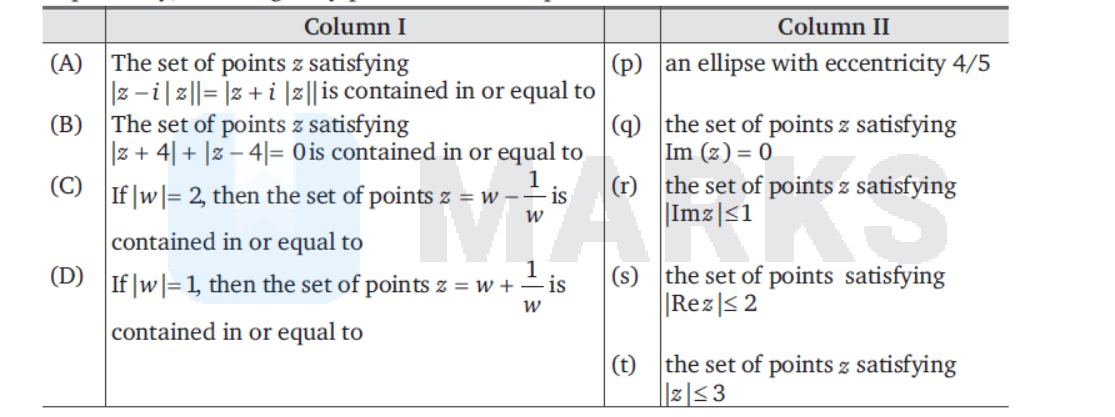
Options:
[Note : Here $z$ takes values in the complex plane and $\operatorname{Im}(z)$ and $\operatorname{Re}(z)$ denote respectively, the imaginary part and the real part of $z$ ]

Solution:
1107 Upvotes
Verified Answer
The correct answer is:
(A) q,r, (B) p, (C) p,s,t, (D) q,r,s,t
(A) q,r, (B) p, (C) p,s,t, (D) q,r,s,t
(A) $z$ is equidistant from the points $i|z|$ and $-i|z|$, whose perpendicular bisector is $\operatorname{Im}(z)=0$.
(B) Sum of distance of $z$ from $(4,0)$ and $(-4,0)$ is a constant 10 , hence locus of $z$ is ellipse with semi-major axis 5 and focus at $(\pm 4,0), a e=4$.
$$
\therefore \quad e=\frac{4}{5}
$$
(C) $|z| \leq|w|+\left|\frac{1}{w}\right|=\frac{5}{2} < 3$
(D) $|z| \leq|w|+\left|\frac{1}{w}\right|=2$
$$
\therefore \quad \operatorname{Re}(z) \leq|z| \leq 2
$$
(B) Sum of distance of $z$ from $(4,0)$ and $(-4,0)$ is a constant 10 , hence locus of $z$ is ellipse with semi-major axis 5 and focus at $(\pm 4,0), a e=4$.
$$
\therefore \quad e=\frac{4}{5}
$$
(C) $|z| \leq|w|+\left|\frac{1}{w}\right|=\frac{5}{2} < 3$
(D) $|z| \leq|w|+\left|\frac{1}{w}\right|=2$
$$
\therefore \quad \operatorname{Re}(z) \leq|z| \leq 2
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.