Search any question & find its solution
Question:
Answered & Verified by Expert
Maximize $Z=3 x+2 y$ subject to $x+2 y \leq 10$, $3 x+y \leq 15, x, y \geq 0$.
Solution:
2017 Upvotes
Verified Answer
Consider $x+2 y \leq 10$
Let $\mathrm{x}+2 \mathrm{y}=10 \Rightarrow \frac{x}{10}+\frac{y}{5}=1$
Now $(0,0)$ satisfies the inequation, therefore the half plane containing $(0,0)$ is the required plane.
Again $3 x+2 y \leq 15$
Let $3 \mathrm{x}+\mathrm{y}=15 \Rightarrow \frac{x}{5}+\frac{y}{15}=1$
It is also satisfies by $(0,0)$ and its required half plane contains $(0,0)$.
Now double shaded region in the first quadrant contains the solution.
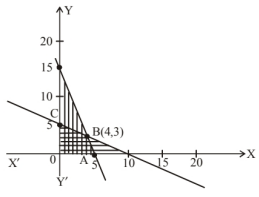
Now $\mathrm{OABC}$, represents the feasible region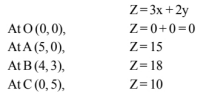
Now $\operatorname{Max} \mathrm{Z}=18$ at $\mathrm{x}=4, \mathrm{y}=3$.
Let $\mathrm{x}+2 \mathrm{y}=10 \Rightarrow \frac{x}{10}+\frac{y}{5}=1$
Now $(0,0)$ satisfies the inequation, therefore the half plane containing $(0,0)$ is the required plane.
Again $3 x+2 y \leq 15$
Let $3 \mathrm{x}+\mathrm{y}=15 \Rightarrow \frac{x}{5}+\frac{y}{15}=1$
It is also satisfies by $(0,0)$ and its required half plane contains $(0,0)$.
Now double shaded region in the first quadrant contains the solution.

Now $\mathrm{OABC}$, represents the feasible region
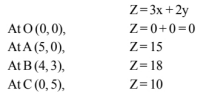
Now $\operatorname{Max} \mathrm{Z}=18$ at $\mathrm{x}=4, \mathrm{y}=3$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.