Search any question & find its solution
Question:
Answered & Verified by Expert
Observe the following complexes
$\begin{aligned}
& {\left[\mathrm{Mn}(\mathrm{CN})_6\right]^{3-},\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{-3},\left[\mathrm{Co}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-},\left[\mathrm{MnCl}_6\right]^{3-},} \\
& {\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4-},\left[\mathrm{CoF}_6\right]^{3-}}
\end{aligned}$
From the above, the number of inner orbital complexes with paramagnetic nature is
Options:
$\begin{aligned}
& {\left[\mathrm{Mn}(\mathrm{CN})_6\right]^{3-},\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{-3},\left[\mathrm{Co}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-},\left[\mathrm{MnCl}_6\right]^{3-},} \\
& {\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4-},\left[\mathrm{CoF}_6\right]^{3-}}
\end{aligned}$
From the above, the number of inner orbital complexes with paramagnetic nature is
Solution:
1522 Upvotes
Verified Answer
The correct answer is:
$2$
$\begin{aligned} & {\left[\mathrm{Mn}(\mathrm{CN})_6\right]^{3-}:-} \\ & \mathrm{Mn}^{3+}=[\mathrm{Ar}]^3 \mathrm{~d}^4\end{aligned}$
$\mathrm{CN}^{-}$is a strong-field ligand so it pairs the electrons.
Thus,
$\left[\mathrm{Mn}(\mathrm{CN})_6\right]^{3-}=$

Thus, it is an inner-orbital but a diamagnetic complex.
$\begin{aligned}
& {\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{3-}:-} \\
& \mathrm{Fe}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^5
\end{aligned}$
$\mathrm{CN}^{-}$will pair - up the electrons so :-
$\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{3-}=$
Thus, it is an inner-orbital and a paramagnetic complex.
$\begin{aligned}
& {\left[\mathrm{Co}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-}:-} \\
& \mathrm{Co}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^6
\end{aligned}$
$\mathrm{C}_2 \mathrm{O}_4{ }^{2-}$ is a weak-field ligand so :-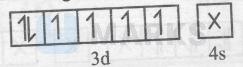
$\left[\mathrm{Co}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-}=$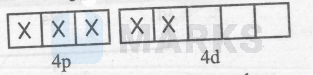
Thus, it is an outer-orbital and paramagnetic complex
$\begin{aligned}
& {\left[\mathrm{MnCl}_6\right]^{3-}:-} \\
& \mathrm{Mn}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^4
\end{aligned}$
$\mathrm{Cl}^{-}$is a weak-field ligand so :-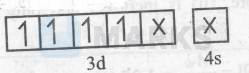
$\left[\mathrm{MnCl}_6\right]^{3-}=$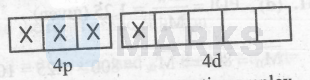
Thus, it is an inner-orbital and paramagnetic complex $\left[\mathrm{Fe}(\mathrm{CN})_6\right]^4$ :-
$\mathrm{Fe}^{2+}=[\mathrm{Ar}] 3 \mathrm{~d}^6$ and $\mathrm{CN}^{-}$is a strong-field ligand.
Thus,
$\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4-}=$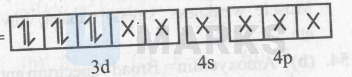
Thus, it is an inner-orbital and diamagnetic complex. $\left[\mathrm{CoF}_6\right]^{3-}:-$ $\mathrm{Co}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^6$ and $\mathrm{F}^{-}$is a weak-field ligand.
Thus,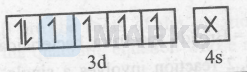
$\left[\mathrm{CoF}_6\right]^{3-}=$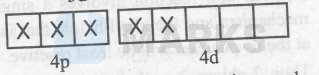
Thus, it is an outer-orbital and paramagnetic complex. Therefore, there are two inner-orbital and paramagnetic complexes.
$\mathrm{CN}^{-}$is a strong-field ligand so it pairs the electrons.
Thus,
$\left[\mathrm{Mn}(\mathrm{CN})_6\right]^{3-}=$

Thus, it is an inner-orbital but a diamagnetic complex.
$\begin{aligned}
& {\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{3-}:-} \\
& \mathrm{Fe}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^5
\end{aligned}$
$\mathrm{CN}^{-}$will pair - up the electrons so :-
$\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{3-}=$

Thus, it is an inner-orbital and a paramagnetic complex.
$\begin{aligned}
& {\left[\mathrm{Co}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-}:-} \\
& \mathrm{Co}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^6
\end{aligned}$
$\mathrm{C}_2 \mathrm{O}_4{ }^{2-}$ is a weak-field ligand so :-

$\left[\mathrm{Co}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-}=$

Thus, it is an outer-orbital and paramagnetic complex
$\begin{aligned}
& {\left[\mathrm{MnCl}_6\right]^{3-}:-} \\
& \mathrm{Mn}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^4
\end{aligned}$
$\mathrm{Cl}^{-}$is a weak-field ligand so :-

$\left[\mathrm{MnCl}_6\right]^{3-}=$

Thus, it is an inner-orbital and paramagnetic complex $\left[\mathrm{Fe}(\mathrm{CN})_6\right]^4$ :-
$\mathrm{Fe}^{2+}=[\mathrm{Ar}] 3 \mathrm{~d}^6$ and $\mathrm{CN}^{-}$is a strong-field ligand.
Thus,
$\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4-}=$

Thus, it is an inner-orbital and diamagnetic complex. $\left[\mathrm{CoF}_6\right]^{3-}:-$ $\mathrm{Co}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^6$ and $\mathrm{F}^{-}$is a weak-field ligand.
Thus,

$\left[\mathrm{CoF}_6\right]^{3-}=$

Thus, it is an outer-orbital and paramagnetic complex. Therefore, there are two inner-orbital and paramagnetic complexes.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.