Search any question & find its solution
Question:
Answered & Verified by Expert
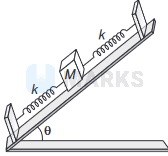
On a smooth inclined plane, a mass \(M\) is attached between two massless springs of force constant \(k\) each, as shown in the figure. The other ends of the springs are fixed to firm supports. The period of oscillation of the mass \(M\) is
Options:

Solution:
1493 Upvotes
Verified Answer
The correct answer is:
\(2 \pi\left(\frac{M}{2 k}\right)^{\frac{1}{2}}\)
According to diagram given in question, it is clear that both springs are connected in series.
\(\therefore\) Equivalent spring constant \(k^{\prime}\) will be
\(k^{\prime}=\frac{k_1 k_2}{k_1+k_2}=\frac{k \cdot k}{k+k}=\frac{k}{2}\) ...(i)
Frequency of oscillation is given as
\(f=\frac{1}{2 \pi} \sqrt{\frac{k^{\prime}}{M}}\)
\(\therefore\) Time period of oscillation,
\(\begin{aligned}
T & =\frac{1}{f}=2 \pi \sqrt{\frac{M}{k^{\prime}}} \\
T & =2 \pi \sqrt{\frac{M}{k / 2}} \quad \text { [from Eq.(i)] } \\
\Rightarrow T & =2 \pi \sqrt{\frac{2 M}{k}}=2 \pi\left(\frac{M}{2 k}\right)^{1 / 2}
\end{aligned}\)
\(\therefore\) Equivalent spring constant \(k^{\prime}\) will be
\(k^{\prime}=\frac{k_1 k_2}{k_1+k_2}=\frac{k \cdot k}{k+k}=\frac{k}{2}\) ...(i)
Frequency of oscillation is given as
\(f=\frac{1}{2 \pi} \sqrt{\frac{k^{\prime}}{M}}\)
\(\therefore\) Time period of oscillation,
\(\begin{aligned}
T & =\frac{1}{f}=2 \pi \sqrt{\frac{M}{k^{\prime}}} \\
T & =2 \pi \sqrt{\frac{M}{k / 2}} \quad \text { [from Eq.(i)] } \\
\Rightarrow T & =2 \pi \sqrt{\frac{2 M}{k}}=2 \pi\left(\frac{M}{2 k}\right)^{1 / 2}
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.