Search any question & find its solution
Question:
Answered & Verified by Expert
One mole of an ideal monoatomic gas undergoes the process $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ as shown in the graph. The work done during the process is
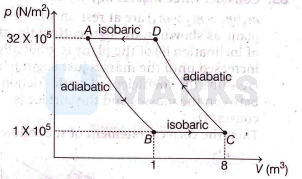
Options:

Solution:
2800 Upvotes
Verified Answer
The correct answer is:
$-52.5 \times 10^5 \mathrm{~J}$
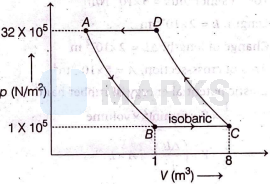
Process undergone by 1 mole gas is as shown
For an ideal monoatomic gas, ratio of specific heat
$\gamma=\frac{5}{3}$
For adiabatic process $A \rightarrow B$
$p_A V_A^\gamma=p_B V_B^\gamma$
Substituting values of $p_A, p_B$ and $V_B$ from graph,
$\Rightarrow \quad 32 \times 10^5 \times V_A^\gamma=1 \times 10^5 \times(1)^\gamma$
$\Rightarrow \quad V_A^\gamma=\left(\frac{1}{32}\right)^\gamma$
Here, $\quad \gamma=\frac{5}{3}$
$\Rightarrow \quad\left(V_A\right)^{\frac{5}{3}}=\frac{1}{32}$
or $V_A=\left(\frac{1}{32}\right)^{\frac{3}{5}}=\frac{1}{\left(2^5\right)^{\frac{3}{5}}}=\frac{1}{8} \mathrm{~m}^3$
Similarly for adiabatic compression $C \rightarrow D$,
$p_C V_C^\gamma=p_D V_D^\gamma$
We substitute values from graph,
$\begin{array}{ll}\Rightarrow & \left(1 \times 10^5\right) \times(8)^{\frac{5}{3}}=\left(32 \times 10^5\right)\left(V_D\right)^{\frac{5}{3}} \\ \Rightarrow & V_D^{5 / 3}=1 \\ \Rightarrow & V_D=1^{3 / 5}=1 \mathrm{~m}^3\end{array}$
Now, Work done in process
$A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$
$=W_{A B}+W_{B C}+W_{C D}+W_{D A}$
Here we substitute work done for adiabatic process,
$W_{\text {adiabatic }}=\frac{p_i V_i-p_f V_f}{\gamma-1}$
and work done of isobaric process,
$W_{\text {isobaric }}=p\left(V_f-V_i\right)$
so, work done in given cycle $A B C D A$
$=W_{A B}+W_{B C}+W_{C D}+W_{D A}$
$\begin{aligned}= & \frac{\left(p_A V_A-p_B V_B\right)}{\gamma-1}+p_B\left(V_C-V_B\right) \\ & \quad+\left(\frac{p_C V_C-p_D V_D}{\gamma-1}\right)+p_D\left(V_A-V_D\right)\end{aligned}$
Substituting values of pressures and volumes, we get
$W_{A B C D A}=\left(\frac{32 \times 10^5 \times \frac{1}{8}-1 \times 10^5 \times 1}{\frac{5}{3}-1}\right)$
$\begin{array}{r}+1 \times 10^5(8-1)+\left(\frac{1 \times 10^5 \times 8-32 \times 10^5 \times 1}{\frac{5}{3}-1}\right) \\ +32 \times 10^5\left(\frac{1}{8}-1\right)\end{array}$
$\begin{aligned}=\frac{3 \times 10^5 \times 3}{2}+7 \times 10^5 & +\frac{-24 \times 10^5 \times 3}{2} \\ & +4 \times 10^5 \times-7=-52.5 \times 10^5 \mathrm{~J}\end{aligned}$

For an ideal monoatomic gas, ratio of specific heat
$\gamma=\frac{5}{3}$
For adiabatic process $A \rightarrow B$
$p_A V_A^\gamma=p_B V_B^\gamma$
Substituting values of $p_A, p_B$ and $V_B$ from graph,
$\Rightarrow \quad 32 \times 10^5 \times V_A^\gamma=1 \times 10^5 \times(1)^\gamma$
$\Rightarrow \quad V_A^\gamma=\left(\frac{1}{32}\right)^\gamma$
Here, $\quad \gamma=\frac{5}{3}$
$\Rightarrow \quad\left(V_A\right)^{\frac{5}{3}}=\frac{1}{32}$
or $V_A=\left(\frac{1}{32}\right)^{\frac{3}{5}}=\frac{1}{\left(2^5\right)^{\frac{3}{5}}}=\frac{1}{8} \mathrm{~m}^3$
Similarly for adiabatic compression $C \rightarrow D$,
$p_C V_C^\gamma=p_D V_D^\gamma$
We substitute values from graph,
$\begin{array}{ll}\Rightarrow & \left(1 \times 10^5\right) \times(8)^{\frac{5}{3}}=\left(32 \times 10^5\right)\left(V_D\right)^{\frac{5}{3}} \\ \Rightarrow & V_D^{5 / 3}=1 \\ \Rightarrow & V_D=1^{3 / 5}=1 \mathrm{~m}^3\end{array}$
Now, Work done in process
$A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$
$=W_{A B}+W_{B C}+W_{C D}+W_{D A}$
Here we substitute work done for adiabatic process,
$W_{\text {adiabatic }}=\frac{p_i V_i-p_f V_f}{\gamma-1}$
and work done of isobaric process,
$W_{\text {isobaric }}=p\left(V_f-V_i\right)$
so, work done in given cycle $A B C D A$
$=W_{A B}+W_{B C}+W_{C D}+W_{D A}$
$\begin{aligned}= & \frac{\left(p_A V_A-p_B V_B\right)}{\gamma-1}+p_B\left(V_C-V_B\right) \\ & \quad+\left(\frac{p_C V_C-p_D V_D}{\gamma-1}\right)+p_D\left(V_A-V_D\right)\end{aligned}$
Substituting values of pressures and volumes, we get
$W_{A B C D A}=\left(\frac{32 \times 10^5 \times \frac{1}{8}-1 \times 10^5 \times 1}{\frac{5}{3}-1}\right)$
$\begin{array}{r}+1 \times 10^5(8-1)+\left(\frac{1 \times 10^5 \times 8-32 \times 10^5 \times 1}{\frac{5}{3}-1}\right) \\ +32 \times 10^5\left(\frac{1}{8}-1\right)\end{array}$
$\begin{aligned}=\frac{3 \times 10^5 \times 3}{2}+7 \times 10^5 & +\frac{-24 \times 10^5 \times 3}{2} \\ & +4 \times 10^5 \times-7=-52.5 \times 10^5 \mathrm{~J}\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.