Search any question & find its solution
Question:
Answered & Verified by Expert
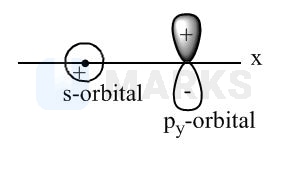
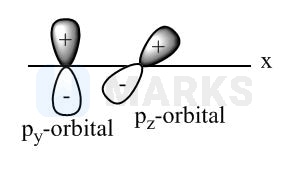
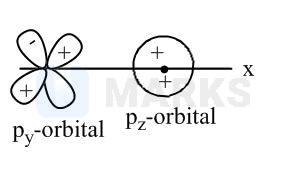
Out of the given ten pairs of combination total pair(s), which results in zero overlapping is: (Assuming \( Z \) is overlapping axis). \( \left(\mathrm{p}_{\mathrm{y}}+\mathrm{s}\right),\left(\mathrm{d}_{\mathrm{xy}}+\mathrm{s}\right),\left(\mathrm{d}_{\mathrm{xy}}+\mathrm{p}_{\mathrm{y}}\right) \) \( \left(\mathrm{p}_{\mathrm{z}}+\mathrm{d}_{\mathrm{xy}}\right),\left(\mathrm{p}_{\mathrm{z}}+\mathrm{s}\right),\left(\mathrm{p}_{\mathrm{y}}+\mathrm{P}_{\mathrm{z}}\right) \) \( (\mathrm{s}+\mathrm{s}),\left(\mathrm{s}+\mathrm{p}_{\mathrm{y}}\right),\left(\mathrm{p}_{\mathrm{y}}+\mathrm{p}_{\mathrm{y}}\right) \)
Solution:
2315 Upvotes
Verified Answer
The correct answer is:
4
No overlapping is possible in the opposite symmetry orbitals (along axis) i.e., .
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.