Search any question & find its solution
Question:
Answered & Verified by Expert
Paragraph:
A uniform thin cylindrical disk of mass $M$ and radius $R$ is attached to two identical massless springs of spring constant $k$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance $d$ from its centre. The axle is massless and both the springs and the axle are in a horizontal plane. The unstretched length of each spring is $L$. The disk is initially at its equilibrium position with its centre of mass $(C M)$ at a distance Lfrom the wall. The disk rolls without slipping with velocity $\mathbf{v}_0=v_0 \hat{\mathbf{i}}$ The coefficient of friction is $\mu$.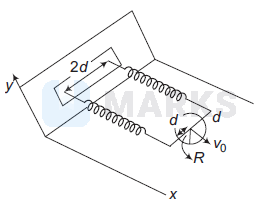
Question:
The centre of mass of the disk undergoes simple harmonic motion with angular frequency $\omega$ equal to
Options:
A uniform thin cylindrical disk of mass $M$ and radius $R$ is attached to two identical massless springs of spring constant $k$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance $d$ from its centre. The axle is massless and both the springs and the axle are in a horizontal plane. The unstretched length of each spring is $L$. The disk is initially at its equilibrium position with its centre of mass $(C M)$ at a distance Lfrom the wall. The disk rolls without slipping with velocity $\mathbf{v}_0=v_0 \hat{\mathbf{i}}$ The coefficient of friction is $\mu$.

Question:
The centre of mass of the disk undergoes simple harmonic motion with angular frequency $\omega$ equal to
Solution:
1442 Upvotes
Verified Answer
The correct answer is:
$\sqrt{\frac{4 k}{3 M}}$
$\sqrt{\frac{4 k}{3 M}}$
$$
\begin{aligned}
& F_{\text {net }}=-\left(\frac{4 k}{3}\right) \cdot x \\
& \therefore a=\frac{F_{\text {net }}}{M}=-\left(\frac{4 k}{3 M}\right) x=-\omega^2 x \\
& \therefore \omega=\sqrt{\frac{4 k}{3 M}}
\end{aligned}
$$
$\therefore$ correct option is (d).
\begin{aligned}
& F_{\text {net }}=-\left(\frac{4 k}{3}\right) \cdot x \\
& \therefore a=\frac{F_{\text {net }}}{M}=-\left(\frac{4 k}{3 M}\right) x=-\omega^2 x \\
& \therefore \omega=\sqrt{\frac{4 k}{3 M}}
\end{aligned}
$$
$\therefore$ correct option is (d).
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.