Search any question & find its solution
Question:
Answered & Verified by Expert
Paragraph:
Consider the circle $x^2+y^2=9$ and the parabola $y^2=8 x$. They intersect at $P$ and $Q$ in the first and the fourth quadrants, respectively. Tangents to the circle at $P$ and $Q$ intersect the $\mathrm{X}$-axis at $R$ and tangents to the parabola at $P$ and $Q$ intersect the $\mathrm{X}$-axis at $S$.Question:
The ratio of the areas of the $\triangle P Q S$ and $\triangle P Q R$ is
Options:
Consider the circle $x^2+y^2=9$ and the parabola $y^2=8 x$. They intersect at $P$ and $Q$ in the first and the fourth quadrants, respectively. Tangents to the circle at $P$ and $Q$ intersect the $\mathrm{X}$-axis at $R$ and tangents to the parabola at $P$ and $Q$ intersect the $\mathrm{X}$-axis at $S$.Question:
The ratio of the areas of the $\triangle P Q S$ and $\triangle P Q R$ is
Solution:
2859 Upvotes
Verified Answer
The correct answer is:
$1: 4$
$1: 4$
Coordinates of $P$ and $Q$ are $(1,2 \sqrt{2})$ and $(1,-2 \sqrt{2})$.
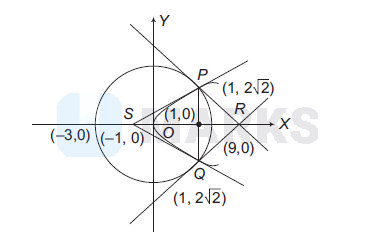
Area of $\triangle P Q R=\frac{1}{2} \cdot 4 \sqrt{2} \cdot 8=16 \sqrt{2}$
Area of $\triangle P Q S=\frac{1}{2} \cdot 4 \sqrt{2} \cdot 2=4 \sqrt{2}$
Ratio of area of $\triangle P Q S$ and $\triangle P Q R$ is $1: 4$.
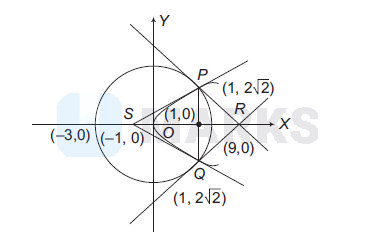
Area of $\triangle P Q R=\frac{1}{2} \cdot 4 \sqrt{2} \cdot 8=16 \sqrt{2}$
Area of $\triangle P Q S=\frac{1}{2} \cdot 4 \sqrt{2} \cdot 2=4 \sqrt{2}$
Ratio of area of $\triangle P Q S$ and $\triangle P Q R$ is $1: 4$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.