Since $x$ lies in fourth quadrant.


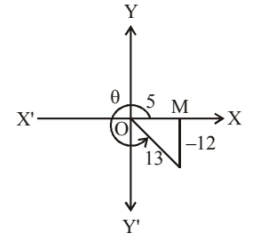
$\therefore \sec x=\frac{13}{5} \Rightarrow \frac{\mathrm{OP}}{\mathrm{OM}}=\frac{13}{5}$
Let $\mathrm{OP}=13, \mathrm{OM}=5$. Then,
$\begin{aligned}
\mathrm{MP} &=-\sqrt{\mathrm{OP}^2-\mathrm{OM}^2} \\
&=-\sqrt{169-25} \\
&=-\sqrt{144}=-12
\end{aligned}$
Now, $\sin x=\frac{\mathrm{MP}}{\mathrm{OP}}=\frac{-12}{13}$
$\cot x=\frac{\mathrm{OM}}{\mathrm{MP}}=\frac{5}{12}=-\frac{5}{12}$
$\cos x=\frac{\mathrm{OM}}{\mathrm{OP}}=\frac{5}{3}$
$\sec x=\frac{\mathrm{OP}}{\mathrm{OM}}=\frac{13}{5}$
$\tan x=\frac{\mathrm{MP}}{\mathrm{OM}}=\frac{-12}{5}$
$\operatorname{cosec} x=\frac{\mathrm{OP}}{\mathrm{MP}}=\frac{13}{-12}=-\frac{13}{12}$