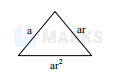
$\mathrm{}$
$$
\begin{array}{l}
a+a r>a r^{2} \\
r^{2}-r-1 < 0 \\
r \in\left(\frac{1-\sqrt{5}}{2}, \frac{1+\sqrt{5}}{2}\right)...(1) \\
a r^{2}+a r>a \\
r^{2}+r-1>0 \\
r>\frac{-1+\sqrt{5}}{2}, r < \frac{-1-\sqrt{5}}{2}...(2)
\end{array}
$$
$\mathrm{ar}^{2}+\mathrm{a}>$ ar ; $\quad \mathrm{r}^{2}-\mathrm{r}+1>0$ always true
ving (1) \& (2)
$$
\mathrm{r} \in\left(\frac{\sqrt{5}-1}{2}, \frac{\sqrt{5}+1}{2}\right)
$$