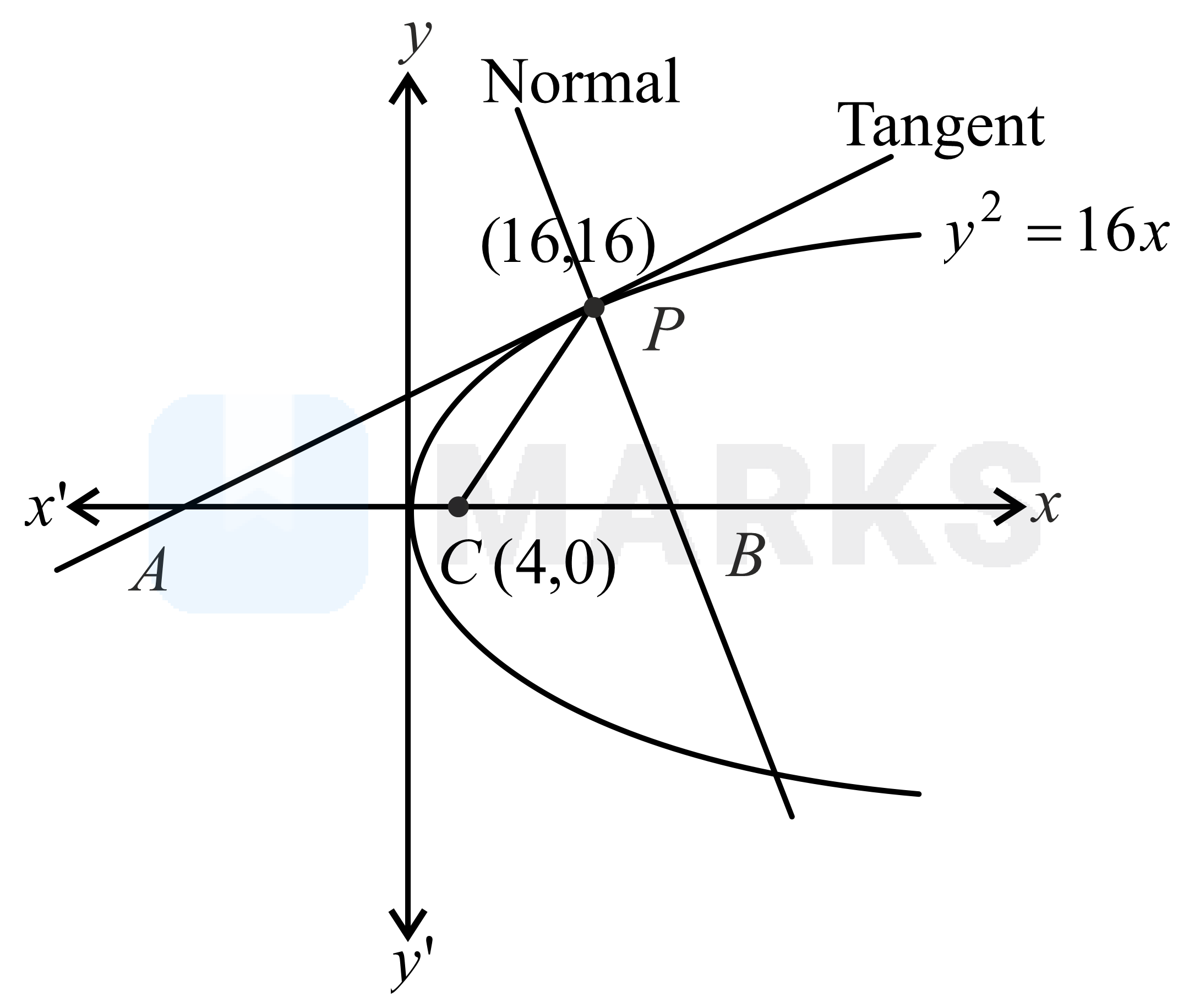
Equation of tangent at $\left(x_1,y_1\right)$ is  $y{y}_1=2a\left(x+x_1\right)$

Equation of normal at $\left(x_1,y_1\right)$ is $y-y_1=-\frac{y_1}{2a}(x-x_1)$

Here tangent and normal passes through $P(16,16)$

$\therefore$ Equation of tangent is $2y=x+16$

Equation of normal is $y+2x=48$

Tangent and normal intersect x-axis at $A\left(-16,0\right)$ and $B(24,0)$

Since, $APB$ is a right angled triangle, hence $AB$ is the diameter for the circle.

Also mid point of $AB$ is center of the circle.

Hence Centre $=\left(4,0\right)$

Slope of $PC$ $=\frac{4}{3}$

Slope of $PB$$=-2$

$\tan \theta =\left|\frac{\frac{4}{3}+2}{1-2\times \frac{4}{3}}\right|=\left|\frac{10}{-5}\right|=2$