Search any question & find its solution
Question:
Answered & Verified by Expert
The area bounded by the parabola $y^{2}=x$, straight line $y=4$ and $y$ -axis is square units is
Options:
Solution:
1865 Upvotes
Verified Answer
The correct answer is:
$64 / 3$ sq. unit
Line $y=4$ meets the parabola $y^{2}=x$ at $A$
$\therefore \quad 16=x$ and $A$ is $(16,4)$
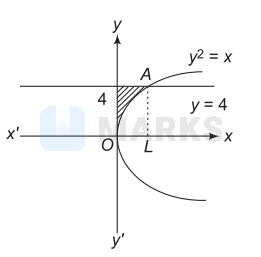
$\therefore$ Required area
$$
\begin{array}{l}
=\int_{y=0}^{4} x d y \\
=\int_{y=0}^{4} y^{2} d y \\
=\left[y^{3} / 3\right]_{0}^{4} \\
=\frac{64}{3} \text { sq units }
\end{array}
$$
$\therefore \quad 16=x$ and $A$ is $(16,4)$

$\therefore$ Required area
$$
\begin{array}{l}
=\int_{y=0}^{4} x d y \\
=\int_{y=0}^{4} y^{2} d y \\
=\left[y^{3} / 3\right]_{0}^{4} \\
=\frac{64}{3} \text { sq units }
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.