We have, $y^{2}=4 x$
Differentiating w.r.t. $x$, we get
$$
\begin{aligned}
&2 y \frac{d y}{d x}=4 \Rightarrow \frac{d y}{d x}=\frac{2}{y} \\
&\left(\frac{d y}{d x}\right)_{(1,2)}=\frac{2}{2}=1
\end{aligned}
$$



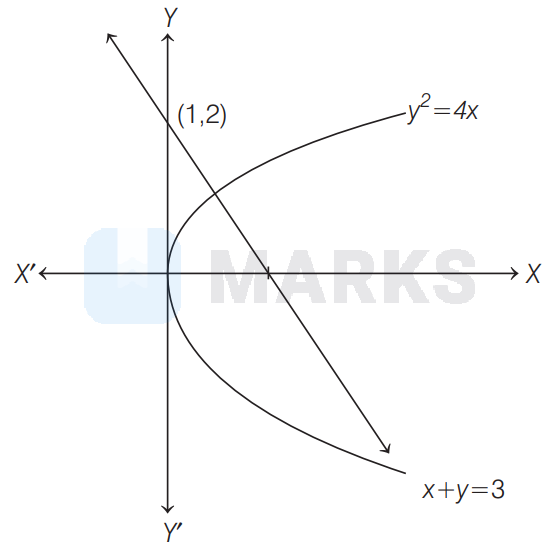
Equation of normal to the curve at $(1,2)$ is
$$
\begin{aligned}
&\begin{aligned}
y-y_{1}=& \frac{1}{\left(-\frac{d y}{d x}\right)}\left(x-x_{1}\right) \Rightarrow(y-2)=-\frac{1}{1}(x-1)
\end{aligned} \\
&\Rightarrow \quad y-2=-x+1 \Rightarrow x+y=3 \\
&\text { The line } x+y=3 \text { meets the X-axis at } x=3 \\
&\therefore \text { Required area }=\int_{0}^{1} \sqrt{4 x} d x+\int_{1}^{3}(3-x) d x \\
&=2\left[\frac{x^{3 / 2}}{3 / 2}\right]_{0}^{1}+\left[3 x-\frac{x^{2}}{2}\right]_{1}^{3} \\
&=\frac{4}{3}(1)+\left[9-\frac{9}{2}-3+\frac{1}{2}\right]=\frac{4}{3}+\left(\frac{9}{2}-\frac{5}{2}\right) \\
&=\frac{4}{3}+\frac{4}{2}=\frac{4}{3}+2=\frac{10}{3} \text { sq units }
\end{aligned}
$$