Search any question & find its solution
Question:
Answered & Verified by Expert
The diagram shows a barrel of weight $1.0 \times 10^{3} \mathrm{~N}$ on a frictionless slope inclined at $30^{\circ}$ to the horizontal.
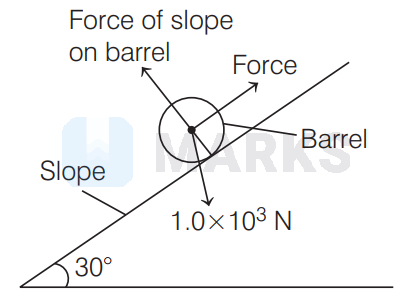
The force is parallel to the slope. What is the work done in moving the barrel a distance of $5.0 \mathrm{~m}$ up the slope?
Options:

The force is parallel to the slope. What is the work done in moving the barrel a distance of $5.0 \mathrm{~m}$ up the slope?
Solution:
1794 Upvotes
Verified Answer
The correct answer is:
$2.5 \times 10^{3} \mathrm{~J}$
The given situation is shown below
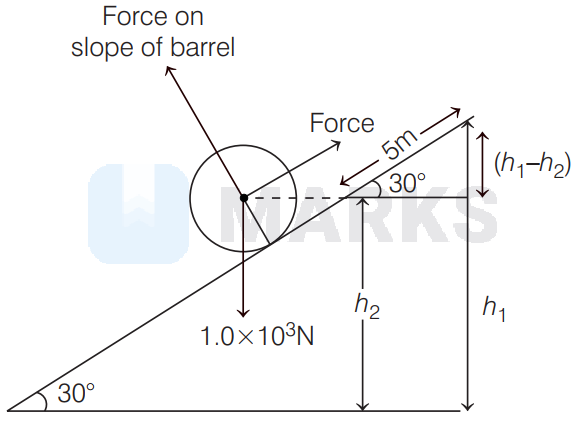
Work done in moving the barrel on the frictionless slope is equal to change in potential energy.
i.e. $W=m g\left(h_{1}-h_{2}\right)$
Here, $\quad m g=1 \times 10^{3} \mathrm{~N}$
From figure, $\sin 30^{\circ}=\frac{h_{1}-h_{2}}{5}$ $\Rightarrow \quad h_{1}-h_{2}=5 \sin 30^{\circ}=\frac{5}{2}=25 \mathrm{~m}$
Putting these values in Eq. (i), we get
$$
W=1 \times 10^{3}(2.5)=2.5 \times 10^{3} \mathrm{~J}
$$

Work done in moving the barrel on the frictionless slope is equal to change in potential energy.
i.e. $W=m g\left(h_{1}-h_{2}\right)$
Here, $\quad m g=1 \times 10^{3} \mathrm{~N}$
From figure, $\sin 30^{\circ}=\frac{h_{1}-h_{2}}{5}$ $\Rightarrow \quad h_{1}-h_{2}=5 \sin 30^{\circ}=\frac{5}{2}=25 \mathrm{~m}$
Putting these values in Eq. (i), we get
$$
W=1 \times 10^{3}(2.5)=2.5 \times 10^{3} \mathrm{~J}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.