Search any question & find its solution
Question:
Answered & Verified by Expert
The electrostatic potential inside a charged sphere is given as $V=A r^2+B$, where $r$ is the distance from the centre of the sphere, $A$ and $B$ are constants. Then, the charge density in the sphere is
Options:
Solution:
1156 Upvotes
Verified Answer
The correct answer is:
$-6 A \varepsilon_0$
Let the volume charge density be $\rho$.
The electric field inside the charged sphere,
$$
E=\frac{K q r}{R^3}
$$
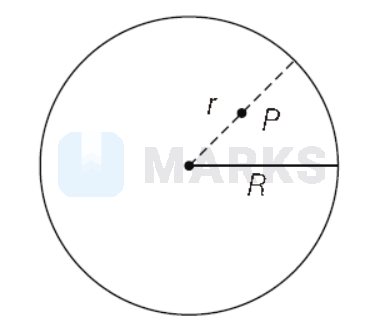
where, $R=$ Radius of charged sphere $r=$ Distance of the point $(P)$ inside the sphere
As volume charge density is $\rho$, then in terms of charge density,
$$
\begin{aligned}
E & =\frac{\rho r}{3 \varepsilon_0} \\
\quad \quad \quad \rho & =\frac{3 E \varepsilon_0}{r}
\end{aligned}
$$
Now, electric field, $E=-\frac{d V}{d r}$
Here, $V=A r^2+B$
$$
\begin{array}{ll}
\therefore & E=-\frac{d V}{d r}=-2 A r+0=-2 A r \\
\therefore & \rho=\frac{3 E \varepsilon_0}{r}
\end{array}
$$
$$
=\frac{3\left(-2 A r \cdot \varepsilon_0\right)}{r}=-6 A \varepsilon_0
$$
The electric field inside the charged sphere,

$$
E=\frac{K q r}{R^3}
$$
where, $R=$ Radius of charged sphere $r=$ Distance of the point $(P)$ inside the sphere
As volume charge density is $\rho$, then in terms of charge density,
$$
\begin{aligned}
E & =\frac{\rho r}{3 \varepsilon_0} \\
\quad \quad \quad \rho & =\frac{3 E \varepsilon_0}{r}
\end{aligned}
$$
Now, electric field, $E=-\frac{d V}{d r}$
Here, $V=A r^2+B$
$$
\begin{array}{ll}
\therefore & E=-\frac{d V}{d r}=-2 A r+0=-2 A r \\
\therefore & \rho=\frac{3 E \varepsilon_0}{r}
\end{array}
$$
$$
=\frac{3\left(-2 A r \cdot \varepsilon_0\right)}{r}=-6 A \varepsilon_0
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.