Search any question & find its solution
Question:
Answered & Verified by Expert
The elevation of an object on a hill is observed from a certain point in the horizontal plane through its base, to be $30^{\circ}$. After walking 120 metres towards it on level ground the elevation is found to be $60^{\circ}$. Then the height of the object (in metres) is :
Options:
Solution:
2498 Upvotes
Verified Answer
The correct answer is:
$60 \sqrt{3}$
Let $h$ be the height of the object.
In $\triangle A C D$
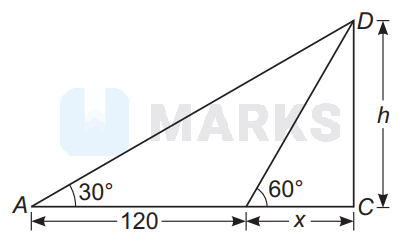
$\tan 30^{\circ}=\frac{C D}{A C}$
$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{120+x}$
$\Rightarrow \quad \sqrt{3} h=120+x$ ...(i)
and in $\triangle B C D$
$\tan 60^{\circ}=\frac{C D}{B C}$
$\Rightarrow \quad \sqrt{3}=\frac{h}{x}$
$\Rightarrow \quad h=\sqrt{3} x$ ...(ii)
From (i) and (ii), we get
$3 x=120+x \Rightarrow x=60$
From Eq. (ii)
Height of the object $=60 \sqrt{3} \mathrm{~m}$.
In $\triangle A C D$

$\tan 30^{\circ}=\frac{C D}{A C}$
$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{120+x}$
$\Rightarrow \quad \sqrt{3} h=120+x$ ...(i)
and in $\triangle B C D$
$\tan 60^{\circ}=\frac{C D}{B C}$
$\Rightarrow \quad \sqrt{3}=\frac{h}{x}$
$\Rightarrow \quad h=\sqrt{3} x$ ...(ii)
From (i) and (ii), we get
$3 x=120+x \Rightarrow x=60$
From Eq. (ii)
Height of the object $=60 \sqrt{3} \mathrm{~m}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.