Search any question & find its solution
Question:
Answered & Verified by Expert
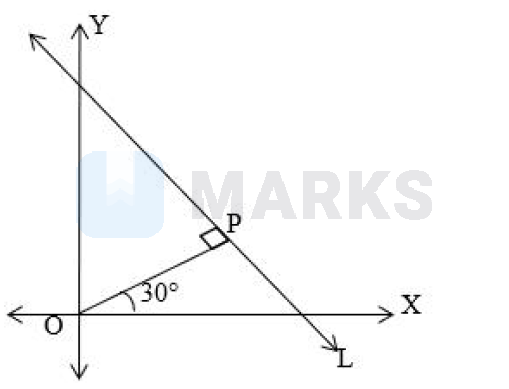
The equation of line, where length of the perpendicular segment from origin to the line is 4 and the inclination of this perpendicular segment with the positive direction of $\mathrm{X}$-axis is $30^{\circ}$, is
Options:
Solution:
2018 Upvotes
Verified Answer
The correct answer is:
$\sqrt{3} x+y=8$
We have $\ell(\mathrm{OP})=4$ and $\mathrm{m} \angle \mathrm{POX}=30^{\circ}$
$$
\therefore \mathrm{P} \equiv\left(4 \cos 30^{\circ}, 4 \sin 30^{\circ}\right) \equiv(2 \sqrt{3}, 2)
$$
From figure, we conclude that angle made be line with +ve $\mathrm{X}$ axis is $120^{\circ}$.
$\therefore$ Slope of line $=\tan \left(120^{\circ}\right)=-\sqrt{3}$
Hence required equation of line $\mathrm{L}$ is
$$
(y-2)=(-\sqrt{3})(x-2 \sqrt{3}) \Rightarrow \sqrt{3} x+y=8
$$

$$
\therefore \mathrm{P} \equiv\left(4 \cos 30^{\circ}, 4 \sin 30^{\circ}\right) \equiv(2 \sqrt{3}, 2)
$$
From figure, we conclude that angle made be line with +ve $\mathrm{X}$ axis is $120^{\circ}$.
$\therefore$ Slope of line $=\tan \left(120^{\circ}\right)=-\sqrt{3}$
Hence required equation of line $\mathrm{L}$ is
$$
(y-2)=(-\sqrt{3})(x-2 \sqrt{3}) \Rightarrow \sqrt{3} x+y=8
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.