Search any question & find its solution
Question:
Answered & Verified by Expert
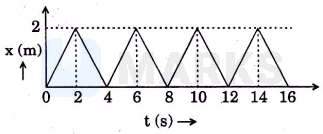
The figure shows the position - time $(x-t)$ graph of one-dimensional motion of a body of mass $0.4 \mathrm{~kg}$. The magnitude of each impulse is
Options:

Solution:
1813 Upvotes
Verified Answer
The correct answer is:
$0.8 \mathrm{Ns}$
$0.8 \mathrm{Ns}$
From the graph, it is a straight line so, uniform motion. Because of impulse direction of velocity changes as can be seen from the slope of the graph.
$$
\begin{aligned}
& \text { Initial velocity }=\frac{2}{2}=1 \mathrm{~m} / \mathrm{s} \\
& \text { Final velocity }=-\frac{2}{2}=-1 \mathrm{~m} / \mathrm{s} \\
& \qquad \bar{P}_{\mathrm{i}}=0.4 \mathrm{~N}-\mathrm{s} \\
& \qquad \overline{\mathrm{P}}_{\mathrm{i}}=-0.4 \mathrm{~N}-\mathrm{s} \\
& \overrightarrow{\mathrm{J}}=\overline{\mathrm{P}}_{\mathrm{i}}-\overline{\mathrm{P}}_{\mathrm{i}}=-0.4-0.4=-0.8 \mathrm{~N}-\mathrm{s}(\overrightarrow{\mathrm{J}}=\text { impulse }) \\
& |\overrightarrow{\mathrm{J}}|=0.8 \mathrm{~N}-\mathrm{s}
\end{aligned}
$$
$$
\begin{aligned}
& \text { Initial velocity }=\frac{2}{2}=1 \mathrm{~m} / \mathrm{s} \\
& \text { Final velocity }=-\frac{2}{2}=-1 \mathrm{~m} / \mathrm{s} \\
& \qquad \bar{P}_{\mathrm{i}}=0.4 \mathrm{~N}-\mathrm{s} \\
& \qquad \overline{\mathrm{P}}_{\mathrm{i}}=-0.4 \mathrm{~N}-\mathrm{s} \\
& \overrightarrow{\mathrm{J}}=\overline{\mathrm{P}}_{\mathrm{i}}-\overline{\mathrm{P}}_{\mathrm{i}}=-0.4-0.4=-0.8 \mathrm{~N}-\mathrm{s}(\overrightarrow{\mathrm{J}}=\text { impulse }) \\
& |\overrightarrow{\mathrm{J}}|=0.8 \mathrm{~N}-\mathrm{s}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.