Search any question & find its solution
Question:
Answered & Verified by Expert
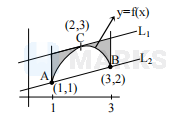
The following figure shows the graph of a continuous function $\mathrm{y}=\mathrm{f}(\mathrm{x})$ on the interval $[1,3]$. The points $\mathrm{A}$, $\mathrm{B}, \mathrm{C}$ have coordinates $(1,1),(3,2),(2,3)$ respectively, and the lines $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$ are parallel, with $\mathrm{L}_{1}$ being tangent to the curve at $\mathrm{C}$. If the area under the graph of $\mathrm{y}=\mathrm{f}(\mathrm{x})$ from $\mathrm{x}=1$ to $\mathrm{x}=3$ is 4 square units, then the area of the shaded region is-
Options:

Solution:
2261 Upvotes
Verified Answer
The correct answer is:
2
Equation of $\ell_{2} \rightarrow \mathrm{y}-1=\frac{2-1}{3-1}(\mathrm{x}-1)$
$2 y-2=x-1$ $2 y-x=1$
Equation of $\ell_{1}=y-3=\frac{1}{2}(x-2)$
$$
\begin{array}{l}
2 y-6=x-2 \\
2 y-x=4 \\
D \rightarrow\left(1, \frac{5}{2}\right), E \rightarrow\left(3, \frac{7}{2}\right)
\end{array}
$$
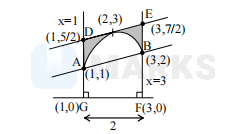
area under $f(x)=4$
$\begin{aligned} \text { shaded area } &=\text { area of trapezium DEFG }-\text { area under } \mathrm{f}(\mathrm{x}) \\ &=\frac{1}{2}\left(\frac{5}{2}+\frac{7}{2}\right) \times 2-4 \\ &=6-4=2 \end{aligned}$
$2 y-2=x-1$ $2 y-x=1$
Equation of $\ell_{1}=y-3=\frac{1}{2}(x-2)$
$$
\begin{array}{l}
2 y-6=x-2 \\
2 y-x=4 \\
D \rightarrow\left(1, \frac{5}{2}\right), E \rightarrow\left(3, \frac{7}{2}\right)
\end{array}
$$

area under $f(x)=4$
$\begin{aligned} \text { shaded area } &=\text { area of trapezium DEFG }-\text { area under } \mathrm{f}(\mathrm{x}) \\ &=\frac{1}{2}\left(\frac{5}{2}+\frac{7}{2}\right) \times 2-4 \\ &=6-4=2 \end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.