Search any question & find its solution
Question:
Answered & Verified by Expert
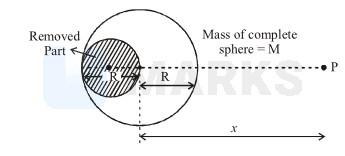
The gravitational field, due to the 'left over part' of a uniform sphere (from which a part as shown, has been 'removed out'), at a very far off point, $\mathrm{P}$, located as shown, would be (nearly) :
Options:

Solution:
1583 Upvotes
Verified Answer
The correct answer is:
$\frac{7}{8} \frac{G M}{x^2}$
$\frac{7}{8} \frac{G M}{x^2}$
Let mass of smaller sphere (which has to be removed) is $\mathrm{m}$
Radius $=\frac{\mathrm{R}}{2}($ from figure $)$
$$
\begin{aligned}
& \frac{\mathrm{M}}{\frac{4}{3} \pi \mathrm{R}^3}=\frac{\mathrm{m}}{\frac{4}{3} \pi\left(\frac{\mathrm{R}}{2}\right)^3} \\
& \Rightarrow \mathrm{m}=\frac{\mathrm{M}}{8}
\end{aligned}
$$
Mass of the left over part of the sphere
$$
\mathrm{M}^{\prime}=\mathrm{M}-\frac{\mathrm{M}}{8}=\frac{7}{8} \mathrm{M}
$$
Therefore gravitational field due to the left over part of the sphere
$$
=\frac{\mathrm{GM}^{\prime}}{\mathrm{x}^2}=\frac{7}{8} \frac{\mathrm{GM}}{\mathrm{x}^2}
$$
Radius $=\frac{\mathrm{R}}{2}($ from figure $)$
$$
\begin{aligned}
& \frac{\mathrm{M}}{\frac{4}{3} \pi \mathrm{R}^3}=\frac{\mathrm{m}}{\frac{4}{3} \pi\left(\frac{\mathrm{R}}{2}\right)^3} \\
& \Rightarrow \mathrm{m}=\frac{\mathrm{M}}{8}
\end{aligned}
$$
Mass of the left over part of the sphere
$$
\mathrm{M}^{\prime}=\mathrm{M}-\frac{\mathrm{M}}{8}=\frac{7}{8} \mathrm{M}
$$
Therefore gravitational field due to the left over part of the sphere
$$
=\frac{\mathrm{GM}^{\prime}}{\mathrm{x}^2}=\frac{7}{8} \frac{\mathrm{GM}}{\mathrm{x}^2}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.