$C_1: x^2+y^2-2 x+2 y-2=0$
$C \equiv(1,-1), r=\sqrt{1^2+(-1)^2+2}=2$
$\Rightarrow(x-1)^2+(y+1)^2=4$ ...(i)
$C_2: x^2+y^2=4$ ...(ii)
$C \equiv(0,0), r=2$


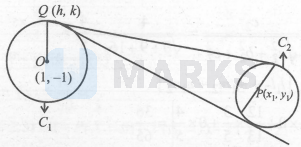
If $P\left(x_1, y_1\right)$ i.e. pole lies outside of the circle then Chord of circle $=$ Locus of polar (i.e. $Q$ )
$\Rightarrow x x_1+y y_1-4=0$ ...(iii)
This is the equation of polar. Perpendicular distance of point $O$ from straight line
$Q S=2=\frac{\left|1 \times x_1-1 \times y_1-4\right|}{\sqrt{x_1^2+y_1^2}}$
Squaring both sides, we get :
$\begin{aligned} & 4\left(x_1^2+y_1^2\right)=\left(x_1-y_1-4\right)^2 \\ & \Rightarrow \quad 4 x_1^2+4 y_1^2=x_1^2+y_1^2+16-2 x_1 y_1+8 y_1-8 x_1 \\ & \Rightarrow \quad 3 x_1^2+3 y_1^2+2 x_1 y_1+8 x_1-8 y_1-16=0\end{aligned}$
Taking locus of the points, we get : $3 x^2+3 y^2+2 x y+8 x-8 y-16=0$