Search any question & find its solution
Question:
Answered & Verified by Expert
The number of distinct positive integers can be formed using $0,1,2,3$ where each integer used at most once is equal to
Options:
Solution:
2034 Upvotes
Verified Answer
The correct answer is:
$48$
Given integers, 0, 1, 2, 3
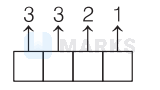
Case I The number of ways to form four digit integers
$=3 \times 3 \times 2 \times 1=18$ (first place can be filled by
one of the three choices $1,2,3)$
Case II The number of 3-digit integers $=3 \times 3 \times 2=18$
Case III The number of 2-digit integers $=3 \times 3=9$
Case IV The number of 1 -digit integer $=3$
$\therefore$ The number of distinct positive integers
$=18+18+9+3=48$

Case I The number of ways to form four digit integers
$=3 \times 3 \times 2 \times 1=18$ (first place can be filled by
one of the three choices $1,2,3)$
Case II The number of 3-digit integers $=3 \times 3 \times 2=18$
Case III The number of 2-digit integers $=3 \times 3=9$
Case IV The number of 1 -digit integer $=3$
$\therefore$ The number of distinct positive integers
$=18+18+9+3=48$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.