Given circle,
$S_1: x^2+y^2-8 x-6 y+21=0$
and $S_2: x^2+y^2-2 y-15=0$
Circle $S_1$ : Centre $C_1(4,3)$, radius $r_1=\sqrt{16+9-21}=2$
$S_2:$ Centre $C_2(0,1)$, radius $r_2=\sqrt{1+15}=4$
Now $\quad C_1 C_2=\sqrt{4^2+2^2}=\sqrt{20}$
$\therefore C_1 C_2 < r_1+r_2 \Rightarrow$ circle $C_1$ and $C_2$ put with other.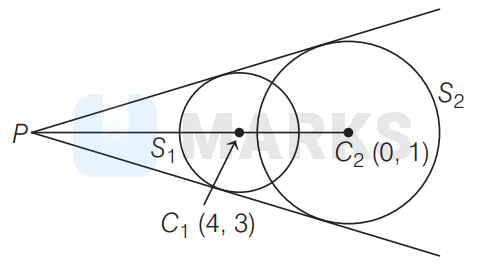

Let point of intersection of tangent on the circle $S_1$ and $S_2$ is $P$.
Now, point $P$ divide line joining $C_2 C_1$ in the ratio of their radii externally
$\therefore \quad \frac{C_2 P}{C_1 P}=\frac{r_2}{r_1} \Rightarrow \frac{C_2 P}{C_1 P}=\frac{4}{2}=\frac{2}{1}$
$\therefore$ By using external division formula
$=\left(\frac{m_1 n_2-m_2 n_1}{m_1-m_2}, \frac{m_1 y_2-m_2 y_1}{m_1-m_2}\right)$
$=\left(\frac{2 \times 4-1 \times 0}{2-1}, \frac{2 \times 3-1 \times 1}{2-1}\right)=(8,5)$