Search any question & find its solution
Question:
Answered & Verified by Expert
The radical centre of three circles described on the three sides of a triangle as diameter is
Options:
Solution:
1078 Upvotes
Verified Answer
The correct answer is:
The orthocentre
Let us consider a triangle as shown in fig.
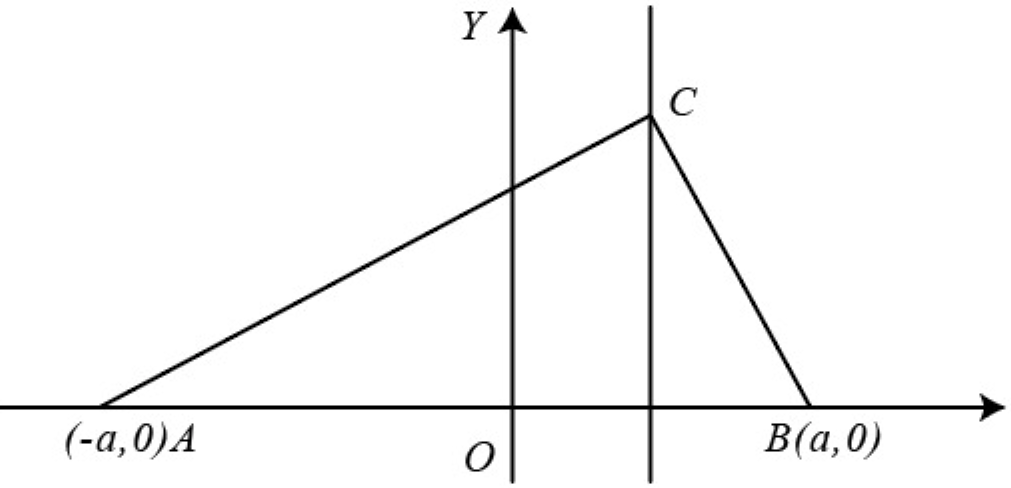
Equations of the circles with $A B, B C$ and $C A$ as diameters are $S_1 \equiv(x+a)(x-a)+y^2=0$
$\begin{aligned} & \qquad S_2 \equiv(x-a)(x-\alpha)+y(y-\beta)=0 \\ & \text { and } S_3 \equiv(x+a)(x-\alpha)+y(y-\beta)=0 \\ & \text { i.e., } S_1 \equiv x^2+y^2-a^2=0\end{aligned}$
$S_2 \equiv x^2+y^2-(a+\alpha) x-\beta y+a \alpha=0$ and $S_3 \equiv x^2+y^2-(\alpha-a) x-\beta y-a \alpha=0$
$\therefore$ Radical axis of $S_2$ and $S_3$ is $S_3-S_2=0$
i.e., $2 a x-2 a \alpha=0$
$\Rightarrow 2 a(x-\alpha)=0, \text { as } a \neq 0, x=\alpha$
But $x=\alpha$ is the orthogonal through $\mathrm{C}$. Similarly other radical axes will be orthogonals through $A$ and $B$. Hence radical ceptre will be the orthocentre.

Equations of the circles with $A B, B C$ and $C A$ as diameters are $S_1 \equiv(x+a)(x-a)+y^2=0$
$\begin{aligned} & \qquad S_2 \equiv(x-a)(x-\alpha)+y(y-\beta)=0 \\ & \text { and } S_3 \equiv(x+a)(x-\alpha)+y(y-\beta)=0 \\ & \text { i.e., } S_1 \equiv x^2+y^2-a^2=0\end{aligned}$
$S_2 \equiv x^2+y^2-(a+\alpha) x-\beta y+a \alpha=0$ and $S_3 \equiv x^2+y^2-(\alpha-a) x-\beta y-a \alpha=0$
$\therefore$ Radical axis of $S_2$ and $S_3$ is $S_3-S_2=0$
i.e., $2 a x-2 a \alpha=0$
$\Rightarrow 2 a(x-\alpha)=0, \text { as } a \neq 0, x=\alpha$
But $x=\alpha$ is the orthogonal through $\mathrm{C}$. Similarly other radical axes will be orthogonals through $A$ and $B$. Hence radical ceptre will be the orthocentre.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.