Search any question & find its solution
Question:
Answered & Verified by Expert
The semivertical angle of a cone is $45^{\circ}$. If the height of the cone is $20.025 \mathrm{~cm}$, then the approximate value of its lateral surface area (in sq. $\mathrm{cm}$ ) is
Options:
Solution:
2628 Upvotes
Verified Answer
The correct answer is:
$401 \sqrt{2} \pi$
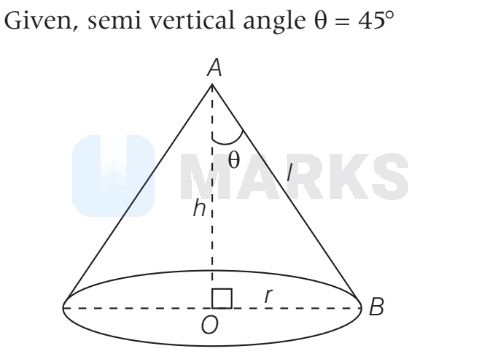
In $\triangle A O B$,
$\begin{aligned}
& \tan 45^{\circ}=\frac{r}{h} \\
& 1=\frac{r}{h} \Rightarrow r=h
\end{aligned}$
and $l^2=r^2+h^2$
$\begin{aligned}
& l=\sqrt{h^2+h^2} \\
& l=\sqrt{2 h^2}=\sqrt{2} h
\end{aligned}$
$[\because r=h]$
Lateral surface area
$\begin{array}{lll}
(S) & =\pi r l & \\
& =\pi h \cdot \sqrt{2} h & \\
S & =\sqrt{2} \pi h^2 & {[\because h=20.025 \mathrm{~cm}]} \\
& =\sqrt{2} \pi(20.025)^2 & \\
& =\sqrt{2} \pi \times 401 & \\
S & =401 \sqrt{2} \pi &
\end{array}$
$\therefore$ Hence, option (a) is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.